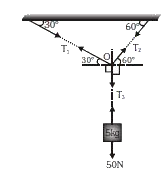
प्रदर्शित चित्र में द्रव्यमान रहित डोरियों में तनाव T1,T2 व T3 की गणना करो। (g=10m/s2)

दिये गये चित्र से
T3 = 5 kg ब्लॉक का भार (mg)
T3 = 5 x 10 = 50 N
बिन्दु O पर लामी प्रमेय का प्रयोग करने पर
T1sin(90∘+60∘)=T2sin(90∘+30∘)=T3sin(180∘−60∘−30∘)
⇒T1cos60∘=T2cos30∘=50sin90∘
⇒T1=50cos60∘sin90∘=25N
T2=50cos30∘sin90∘=25√3N
Topper's Solved these Questions
- न्यूटन के गति के नियम तथा घर्षण Book:ALLEN HINDIChapter:न्यूटन के गति के नियम तथा घर्षण Exercise:BEGINNER.S BOX-1
Explore 10 Videos
- न्यूटन के गति के नियम तथा घर्षण Book:ALLEN HINDIChapter:न्यूटन के गति के नियम तथा घर्षण Exercise:BEGINNER.S BOX-4
Explore 7 Videos
- नाभिकीय भौतिकी तथा रेडियो सक्रियता Book:ALLEN HINDIChapter:नाभिकीय भौतिकी तथा रेडियो सक्रियता Exercise:Exercise-IV (Assertion & Reason)
Explore 25 Videos
- पदार्थो के गुण एवं तरल यांत्रिकी Book:ALLEN HINDIChapter:पदार्थो के गुण एवं तरल यांत्रिकी Exercise:EXERCISE-IV (Assertion & Reason)
Explore 34 Videos
Similar Questions
72 डाइन बल क्षैतिज से 60∘ कोण पर लग रहा है, इस बल के प्रभाव में क्षैतिज दिशा में गति कर रहे 9 ग्राम द्रव्यमान के कण का त्वरण cm/s2 में ज्ञात कीजिये।
View Solutionनिकाय का त्वरण, रस्सी में तनाव तथा घिरनी पर प्रणोद (धक्का) ज्ञात कीजिये ( g के रूप में), चित्र मे प्रदर्शित ब्लाको का द्रव्यमान उपयुक्त इकाई मे है।
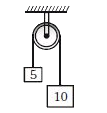
View Solutionकथन: प्रोटॉन की अपेक्षा न्यूट्रान पदार्थ का अधिक भेदन करते है।
कारण :प्रोटॉन की अपेक्षा न्यूट्रॉन कुछ अधिक भारी होते है।
View Solutionकथन :- प्रत्यास्थ प्रत्यानयन बल संरक्षी बल हो सकते हैं।
कारण :- भार बढ़ाते हुए व घटाते हुए समान प्रतिबल पर उत्पन्न विकृति के मान क्रमशः भिन्न-भिन्न होते हैं
View Solutiont1=(sinθ)cosθ,t2=(sinθ)sinθ,t3=(cosθ)cosθ,t4=(cosθ)sinθ (A) t3>t1>t2 (B) t4>t2>t1 (C) t4>t1>t2 (D) t1>t3>t2
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)], [a t_2t_3,a(t_2 +t_3)], [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+at1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionThe vertices of a triangle are [at1t2,a(t1+t2)], [at2t3,a(t2+t3)], [at3t1,a(t3+t1)] Then the orthocenter of the triangle is: (a) (−a,a(t1+t2+t3)−at1t2t3) (b) (−a,a(t1+t2+t3)+a(t1t2t3) (c) (a,a(t1+t2+t3)+at1t2t3) (d) (a,a(t1+t2+t3)−at1t2t3)
View SolutionWrite the correct number in the given blanks from the following A.P.1,8,15,22. a=... t1=....,t2=....,t3=.... t2−t1=....andt3−t2=...., hence d=....
View SolutionWrite the correct number in the given blanks from the following A.P.3,6,9,12. a=... t1=....,t2=....,t3=.... t2−t1=....andt3−t2=...., hence d=....
View SolutionWrite the correct number in the given blanks from the following A.P.70,60,50,40. a=... t1=....,t2=....,t3=.... t2−t1=....andt3−t2=...., hence d=....
View SolutionIf t1,t2 and t3 are distinct, the points (t1,2at1+at31),(t2,2at2+at32),(t3,2at3+at33) are collinear then show that t1+t2+t3=0.
View SolutionThe vertices of a triangle are
[at1t2,a(t1+t2)],[at2t3,a(t2+t3)],[at3t1,a(t3+t1)]
Find the orthocentre of the triangle.
View SolutionArea of the triangle formed by the threepoints 't1'.'t2'and't3' on y2=4ax is K|(t1−t2)(t2−t3)(t3−t1)| then K=
View SolutionThe vertices of a triangle are [a t_1t_2,a(t_1 +t_2)] , [a t_2t_3,a(t_2 +t_3)] , [a t_3t_1,a(t_3 +t_1)] Then the orthocenter of the triangle is (a) (-a, a(t_1+t_2+t_3)-at_1t_2t_3) (b) (-a, a(t_1+t_2+t_3)+at_1t_2t_3) (c) (a, a(t_1+t_2+t_3)+at_1t_2t_3) (d) (a, a(t_1+t_2+t_3)-at_1t_2t_3)
View Solution

