Select the correct statements for hydrogen like atoms or ions.Solution in Telugu
Radius of an orbit is inversely proportional to Z
Radius of an orbit is inversely proportional to Z2
Energy of the electron in an orbit is inversely proportional Z
Energy of the electron in an orbit is directly proportional Z2
The correct Answer is:C, D
Step by step video, text & image solution for Select the correct statements for hydrogen like atoms or ions. by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ATOMIC STRUCTUREBOOK - AAKASH SERIESCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - II (Type-I) (Practice sheet - 2 (Section - B : Linked comprehension Type questions))
5 Videos
- ATOMIC STRUCTUREBOOK - AAKASH SERIESCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - II (Type-I) (Practice sheet - 2 (Section -C : Matching/Straight objective type questions))
2 Videos
- ATOMIC STRUCTUREBOOK - AAKASH SERIESCHAPTER - ATOMIC STRUCTUREEXERCISE - Level - II (Type-I) (Lecture Sheet - 2 (Section -C : Matching/Straight objective type questions))
2 Videos
- AROMATIC HYDROCARBONSBOOK - AAKASH SERIESCHAPTER - AROMATIC HYDROCARBONSEXERCISE - OBJECTIVE EXERCIES - 3 (RECENT AIPMT/NEET QUESTIONS)
10 Videos
- CHEMICAL BONDINGBOOK - AAKASH SERIESCHAPTER - CHEMICAL BONDINGEXERCISE - OBJECTIVE EXERCISE -3 (RECENT AIPMT/NEET QUESTIONS )
39 Videos
Similar Questions
Atoms more complicated than hydrogen have more than one proton in their nucleus. Let Z stands for the number of protons in a nucleus. Also imagine that an atom loses all but one of its electrons so that it changes into a positively charged ion with just one electron. Bohr.s formula for the energy levels of the hydrogen atom can easily be changed to apply to such ions. It becomes Em=−Z2e4me8ε20h2n2, where m= mass of electron , e= change of electron, n = orbit number.
The ionization potential of Het in ground state is
View SolutionIf in Bohr.s model, for uni electronic atom following symbols are used :
rn,Z→ Radius of nth orbit with atomic number z
Un,Z→ Potential energy of e−
Kn,Z→ Kinetic energy of e−
Vn,Z→ Velocity of e−
Tn,Z→ Time period of revolution

View SolutionAccording to Bohr.s theory, En = total energy, Kn = kinetic energy , Vn = potential energy, rn = radius of nth orbit. Match the following.
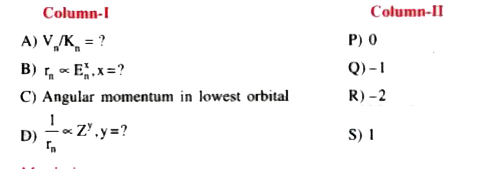
View SolutionUsing anhydrous AICI3 as catalyst which one of the following reactions produces ethyl benzene
View SolutionIn which of the following pairs, the two species are isostructural?
View SolutionThe wavelength of the first line of Lyman series for hydrogen atom is equal to that of the second line of Balmer series for a hydrogen-like ion. The atomic number Z of hydrogen-like ion is
View SolutionWhich statement about the radii of atoms and their ions is correct?
View Solutionthe wavelength of the first line of lyman series for hydrogen atom is equal to that of the second line of balmer series for a hydrogen like ion. The atomic number Z of hydrogen like ion is
View SolutionThe wavelength of the first line of Lyman series for hydrogen atom is equal to that of the second line of Balmer series for a hydrogen like ion. The atomic number Z of hydrogen like ion is
View SolutionThe wavelength of the first line of Lyman series for hydrogen atom is equal to that of the second line of Balmer series for a hydrogen like ion. The atomic number Z of hydrogen like ion is
View SolutionSeparation energy of a hydrogen like ion from its third excited state is 2.25 times the separation energy of hydrogen atom from its first excited state. Find out the atomic number of this hydrogen like ion.
View SolutionThe wavelength of the first line of Lyman series for hyrogen atom is equal to that of the second line of Balmer series for a hydrogen like ion. The atomic number Z of hydrogen like ion is
View Solution
For above transition in hydrogen like atoms, select the correct relations(s).
View Solution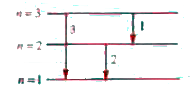
For above transitions in hydrogen like atoms, select the incorrect relation(s).
View Solutionthe wavelength of the first line of lyman series for hydrogen atom is equal to that of the second line of balmer series for a hydrogen like ion. The atomic number Z of hydrogen like ion is
View Solution
