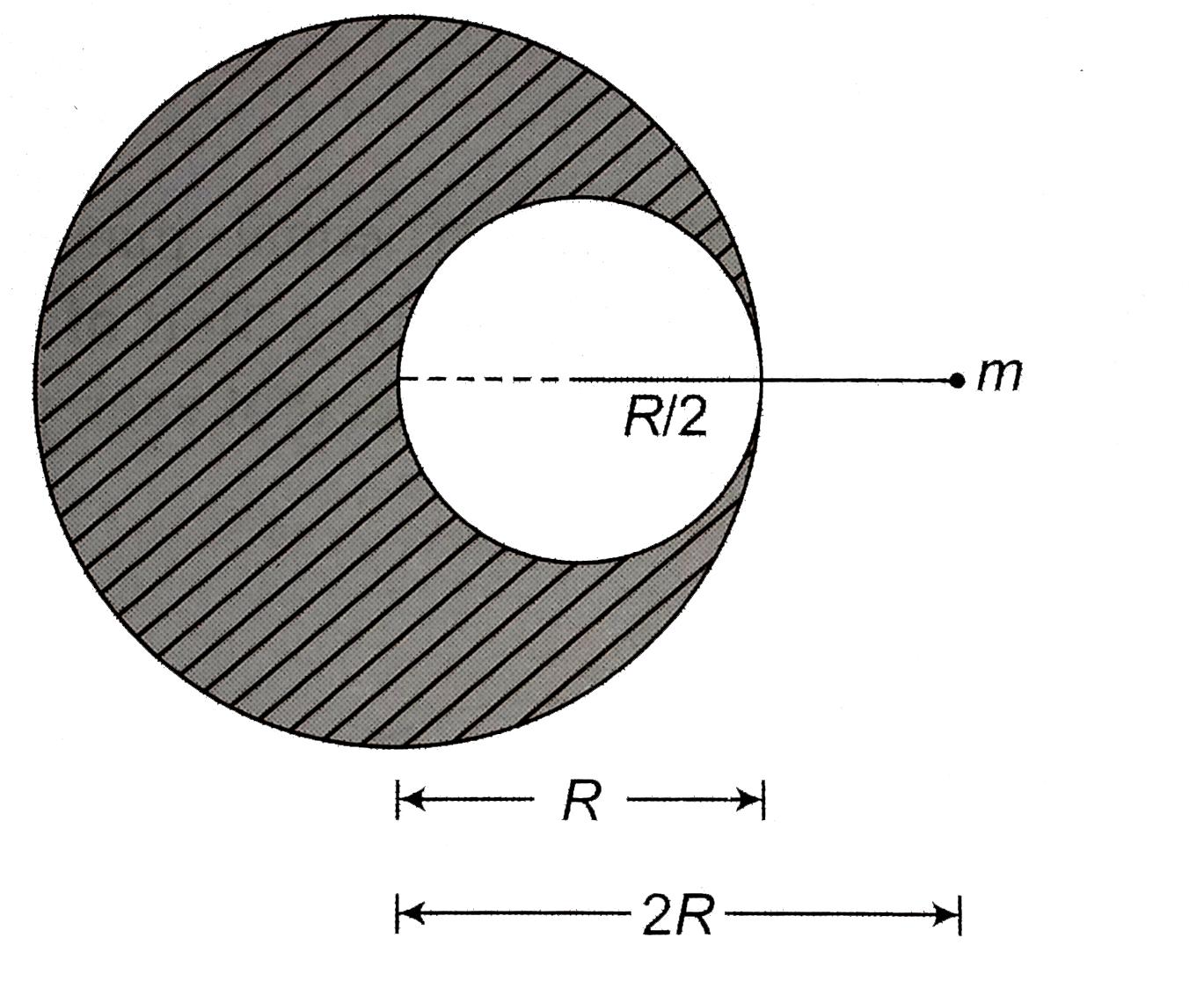
From a solid sphere of mass M and radius R2 aspherical portion of radius ž is romoved as shown in figure. Taking gravitational potential V = 0 and r=∞ , the potential at the centre of the cavity thus form is ......... . (G = Gravitational constant) Solution in Gujrati
−GM2R
−GMR
−2GM3R
−2GMR
The correct Answer is:B
⇒ Gravitational potential of earth (sphere) is V1=GM2R3(3R2−r2),r=R2
V1=−GM2R3[3R2−R24] ...(1)
and Gravitational potenital of portion R2
V2=−3GM82(R2)
Now , V=V1−V2
=−3GM2R+GM8R+3GM8R
=−12GM+GM+3GM8R
=−8GM8R
=−GMR

Topper's Solved these Questions
- GRAVITATIONBook:KUMAR PRAKASHANChapter:GRAVITATIONExercise:Section - F Questions from Module
Explore 20 Videos
- GRAVITATIONBook:KUMAR PRAKASHANChapter:GRAVITATIONExercise:QUESTIONS PAPER Section - A
Explore 6 Videos
- GRAVITATIONBook:KUMAR PRAKASHANChapter:GRAVITATIONExercise:Section - D NCERT Exemplar Solutions (Long Answer Type Question )
Explore 5 Videos
- LAW OF MOTIONBook:KUMAR PRAKASHANChapter:LAW OF MOTIONExercise:(QUESTION PAPER) SECTION-D
Explore 1 Video
Similar Questions
Two particles of equal mass m move around a circle of radius R under the influence of their mutual gravitational attraction, the speed of each particle with respect to their center of mass will be ..........
View SolutionThe magnitude of gravitational intensity at a point is 0.7 N/kg. What would be the magnitude of the gravitational force on a body of 5 kg mass at this point ?
View SolutionA star like the sun has several bodies moving around it at different distances. Consider that all of them are moving in circular orbits. Letr be the distance of the body from the centre of the star and let its linear velocity be v, angular velocity , ω kinetic energy K, gravitational potential energy U, total energy E and angular momentum I. As the radius r of the orbit increases, determine which of the above quantities increase and which ones decrease. As shown in figure, where a body of mass m is revolving around a star of mass M. Linear velocity of the body,
View SolutionA 70 kg man stands in contact against the inner wall of a hollow cylindrical drum of radius 3 m rotating about its vertical axis with 200 rev/min. The coefficient of friction between the wall and his clothing is 0.15. What is the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall (without falling) when the floor is suddenly removed ?
View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V =0at r = oo, the potential at (G = gravitational constatn)
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionFrom a solid sphere of mass M and radius R, a solid sphere of radius R/2 is removed as shown. Find gravitational force on mass m as shown
View SolutionThere is a concentric hole of radius R in a solid sphere of radius 2R. Mass of the remaining portional is M. What is the gravitational potential at centre?
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
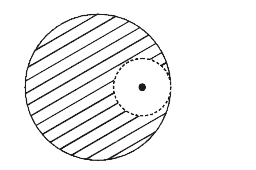
View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radiu R2 is removed as shown in the figure. Taking gravitational potential V = 0 at r=∞, the potential at the centre of the cavity thus formed is (G = gravitational constant)
View Solutionएक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है | इससे त्रिज्या R/2 का एक गोलीय भाग चित्र 9.21 के अनुसार काट लिया जाता है |r=∞ ( अनन्त ) पर गुरुत्वीय विभव के V मान को शून्य (V = 0 ) मानते हुए, इस प्रकार बने कोटर ( कैविटी ) के केंद्र पर, गुरुत्वीय विभव होगा :
View Solutionएक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है । इससे R2 त्रिज्या का एक गोलीय भाग चित्रानुसार काट लिया जाता है । =r=∞ ( अनंत ) पर गुरुत्वीय विभव को V मानते हुए इस प्रकार बने कोटर ( Cavity ) के केंद्र पर गुरुत्वीय विभव का मान होगा ( G गुरुत्वीय नियतांक है )

View Solutionएक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है। इससे - R2त्रिज्या का एक गोलीय भाग, आरेख में दर्शाये गये अनुसार काट लिया जाता है| r=∞(अनन्त) पर गुरुत्वीय विभव के मान V को शून्य (V=0) मानते हुए इस प्रकार बने कोटर (कैविटी) के केन्द्र पर, गुरुत्वीय विभव का मान होगा-

View SolutionFrom a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure Taking gravitational potential V =0at r = oo, the potential at (G = gravitational constatn)
View SolutionM द्रव्यमान व R त्रिज्या के एक ठोस गोले से R2 त्रिज्या का एक गोल क्षेत्र चित्र में दर्शाये अनुसार हटाया जाता है। r=∞ पर गुरूत्वीय विभव V = 0 लीजिये। इस प्रकार बनी गुहा के केन्द्र पर विभव है : (G = गुरूत्वीय नियतांक)

View Solution