Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses and the tension in the string when the masses are released.Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

Let $m_{1} = 8 k g m_{2} = 12 k g$
Let tension in string be T

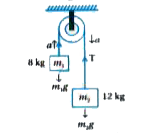
Let common acceleration of system is a
Acceleration of $m_{1}$ is in upward direction acceleration of $m_{2}$ is in downward direction equation of motion of $m_{1}$
By taking addition of equation (1) and (2) we get common acceleration of system
$(m_{2} - m_{1}) g = (m_{1} + m_{2}) a$
$= (\frac{12 - 8}{8 + 12}) \times 10$
$T = m_{1} g + m_{1} (\frac{m_{2} - m_{1}}{m_{1} + m_{2}}) g$
$T = (\frac{2 m_{1} m_{2}}{m_{1} + m_{2}}) g$
Substituting value
$T = \frac{2 \times 8 \times 12}{8 + 12} \times 10$
$T = \frac{2 \times 960}{20}$
$∴ T = 96 N$
Let mass of nucleus is m and initial velocity v= 0
initial momentum ${\vec{p}}_{1} = - m V = 0$
After disintergration it is divided into two part let mass be $m_{1}$ and $m_{2}$ and velocity be ${\vec{v}}_{1}$ and $\vec{2}$ respectively
By law of conservation of linear momentum
${\vec{p}}_{1} = {\vec{p}}_{f}$
$∴, m_{2} v_{2} = - m_{1} m_{1}$
Negative sigh shows that velocity of both fragment are in mutually opposite direction

Updated on:21/07/2023

|

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

KUMAR PRAKASHAN-LAW OF MOTION-SECTION -B (NUMERICAL FROM TEXTUAL EXERCISE)

Home
Ask Doubt
Profile