A body of mass m is situated in a potential field U(x)=U0(1−cosαx) when U0 and α are constants. Find the time period of small oscillations.Solution in Gujrati
Potential energy associated with field U(x)=U0[1−cosαx]
Differentiate w.r.t. to x,
dU(x)dx=ddx[U0(1−cosαx)]
∴−F=−U0α(−sinαx)
∴F=−U0αsinαx
If αx is very small, then sinαx≈αx
∴F=−U0α(αx)=−U0α2x.....(1)
∴F∝(−x) [∴U0,α are constant ]
For small oscillation motion is SHM,
Standard form of force exerted on body performing SHM
F=−mω2x ..........(2)
Comparing equation (1) and (2)
mω2=U0α2
∴ω2=U0m0α2
∴ω=√U0mα2
∴2πT=√U0mα2
∴T=2π√mU0α2.
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-D (NCERT EXEMPLAR SOLUTION LONG ANSWER QUESTIONS)
8 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-E (MCQs ASKED IN GUJARAT BOARD AND COMPETITIVE EXAMS)
66 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
10 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
A person normally weighing 50kg stands on a massless platform which oscillates up and down harmonically at a frequency of 2.0s−1 and an amplitude 5.0cm. A weighing machine on the platform gives the persons weight against time.
Will there be any change in weight of the body, during the oscillation?
View SolutionA particle executes SHM along X-axis. The force acting on it is given by……….
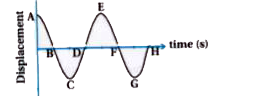
View SolutionDisplacement versus time curve for a particle executing SHM is shown in figure. Idendify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA partical of mass m is located in a unidimensionnal potential field where potentical energy of the partical depends on the coordinates x as: U (x) = U_(0) (1 - cos Ax), U_(0) and A constants. Find the period of small oscillation that the partical performs about the equilibrium position.
View SolutionA body of mass m is situated in a potential field U(x)=U_(0)(1-cosalphax) when U_(0) and alpha are constant. Find the time period of small oscialltions.
View SolutionA particle of mass m is moving in a potential well, for which the potential energy is given by U(x)=U0(1−cosax) where U0 and a are positive constants. Then (for the small value of x)
View SolutionA particle of mass m is located in a potential field given by U (x) = U_(o) (1-cos ax) where U_(o) and a are constants and x is distance from origin. The period of small oscillations is
View SolutionA body of mass m is situated in potential field U(x)=U_(o)(1-cospropx) when, U_(o) and prop are constants. Find the time period of small oscillations.
View SolutionThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x)=0[1−cosax], where U0 and a are constants. The time period of small oscillations of the particle about the mean positions is :
View SolutionThe potential energy of a peticle of mass 'm' situated in a unidimensional potential field varies as U(x) = 0 [1 - cos ax] , where U_(0) and a are constants. The time period of small oscillations of the particle about the mean positions is :
View SolutionA body of mass m is situated in a potential field U(x) = V0(1−cosax) when U0 and α are constants. Find the time period of small oscillations.
View SolutionA particle of mass m oscillates with a potential energy U=U_(0)+alpha x^(2) , where U_(0) and alpha are constants and x is the displacement of particle from equilibrium position. The time period of oscillation is
View Solutionमूल बिन्दु से x दुरी पर स्थित द्रव्यमान m की स्थितिज ऊर्जा U(x)=U0(1−cosαx) है, जहाँ पर U0 व α नियतांक है। अल्प आयाम के दोलनों का आवर्तकाल क्या होगा ?
View Solution
