The displacement of a particle represented by the equation y=3cos(π4−2ωt). The motion of the particle is Solution in Gujrati
simple harmonic with period 2πω
simple harmonic with period πω
periodic but not simple harmonic
non-periodic
The correct Answer is:B
The displacement of motion of particle
y=3cos(π4−2ωt)
∴v=ddt[3cos(π4−2ωt)]
=3(−2ω)[−sin(π4−2ωt)]
∴v=6ωsin(π4−2ωt)
Acceleration, a=dvdt=ddt[6ωsin(π4−2ωt)]
∴a=6ω×(−2ω)cos(π4−2ωt)
=−12ω2cos(π4−2ωt)
=−4ω2[3cos(π4−2ωt)]
∴a=−4ω2y ........(1)
∴a∝−y
This is condition of simple harmonic motion, the motion is SHM and
ω.=2ω [∴ Comparing equation (1) with a=−(ω.)2y]
∴2πT.=2ω
∴T.=2π2ω=πω
Topper's Solved these Questions
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-D (NCERT EXEMPLAR SOLUTION MCQs MORE THAN ONE OPTIONS)
Explore 8 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-D (NCERT EXEMPLAR SOLUTION VERY SHORT ANSWER QUESTIONS)
Explore 10 Videos
- OSCILLATIONSBook:KUMAR PRAKASHANChapter:OSCILLATIONSExercise:SECTION-C (OBJECTIVE QUESTIONS ASSERTION OR REASION)
Explore 7 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Book:KUMAR PRAKASHANChapter:OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE Exercise:CHAPTER - 8 (Match Type questions)
Explore 5 Videos
- PHYSICAL WORLDBook:KUMAR PRAKASHANChapter:PHYSICAL WORLDExercise:SECTION-E (QUESTIONS FROM MODULE)
Explore 9 Videos
Similar Questions
When a mass m is connected individually to two springs S1 and S2 the oscillation frequencies are v1 and v2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be

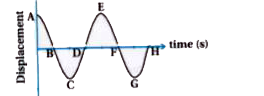
View SolutionDisplacement versus time curve for a particle executing SHM is shown in figure. Idendify the points marked at which (i) velocity of the oscillator is zero, (ii) speed of the oscillator is maximum.
View SolutionAssertion : All oscillatory motions are necessarily periodic motion but all periodic motion are not oscillatory.
Reason : Simple pendulum is an example of oscillatory motion.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionA particle move along y-axis according to equation y+3+4cosωt. The motion of the particle is
View SolutionA x and y co-ordinates of a particle are x=A sin (omega t) and y = A sin(omegat + pi//2) . Then, the motion of the particle is
View Solutionएक कण को दो विस्थापन दिए गए है जिनके समीकरण x1=Acosωt तथा x2=2Acos(ωt+π/3) है। इनके परिणामी विस्थापन दिए गए है जिनके समीकरण तथा है। इनके परिणामी विस्थापन का समीकरण निकालें।
View SolutionThe displacement of a particle is represented by the equation
y=0.4{cos2(πt2)−sin2(πt2)}metre
The motion of the particle is
View SolutionEquations y = 2 A cos2ωt and y = A(sinωt+√3cosωt) represent the motion of two particles.
View SolutionEquations y=2 A cos^2 omega t and y = A ( sin omega t + sqrt3 cos omega t) represent the motion of two particles.
View SolutionThe displacement of a particle is represented by the equation y=sin3ωt. The motion is………..
View SolutionThe displacement of a particle is represented by the equation y=3cos(π4−2ωt).
The motion of the particle is
View SolutionThe displacement of particle is represented by the equation y=3cos(π4−2ωt). The motion of the particle is
View SolutionThe displacement of particle is represented by the equation y=3cos((pi)/4-2omegat) . The motion of the particle is
View Solution

