The motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.Solution in Gujrati
x(t)=Acos(ωt(+ϕ)
x(0)=Acosϕ [∴t=0]
∴1=Acosϕ ……….(1) [x(0)=1cm]
Also, diffrerentiating this equation. ω.r.t..t..
v(t)=−Aωsin(ωt+ϕ)
∴v(0)=−Aωsinϕ [∴t=0]
∴ω=−Aωsinϕ [∴v(0)=ω]
∴1=−Asinϕ ........(2)
Squaring and adding equn. (1) and (2)
1+1=A2cos2ϕ+A2sin2ϕ
∴2=A2 [∴cos2ϕ+sin2ϕ=1]
∴A=±√2cm
Dividing eqn. (2) by (1),
−1=tanϕ⇒tanϕ=−1
∴tanϕ=−tan(π)4
tanϕ=tan(2π−π4)
∴ϕ=2π−π4
∴ϕ=7π4rad
Now let consider x(t)=Bsin(ωt+α)
x(0)=Bsinα [∴t=0]
1=Bsinα ........(3)[∴x(0)=1]
and differentiating this equation ω.r.t..t.,
v(t)=Bωcos(ωt+α)
v(0)=Bωcosα [∴t=0]
∴ω=Bωcosα [∴v(0)=ω]
∴1=Bcosα ......(4)
Squaring and adding equn. (3) and (4),
12+12=B2sin2α+B2cos2α
∴1+1=B2[sin2α+cos2α]
∴2=B2 [∴sin2α+cos2α=1]
∴B=±√2cm
Diving (3) and (4),
1=tanα
∴α=tan−1(1)
∴α=π4rad
Topper's Solved these Questions
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (ADDITIONAL EXERCISE)
9 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM DARPAN BASED ON TEXTBOOK)
15 Videos
- OSCILLATIONSBOOK - KUMAR PRAKASHANCHAPTER - OSCILLATIONSEXERCISE - SECTION-B (NUMERICAL FROM TEXTUAL ILLUSTRATIONS)
40 Videos
- OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE BOOK - KUMAR PRAKASHANCHAPTER - OBJECTIVE QUESTIONS AS PER NEW PAPER STYLE EXERCISE - CHAPTER - 8 (Match Type questions)
5 Videos
- PHYSICAL WORLDBOOK - KUMAR PRAKASHANCHAPTER - PHYSICAL WORLDEXERCISE - SECTION-E (QUESTIONS FROM MODULE)
9 Videos
Similar Questions
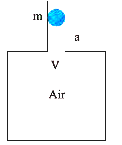
An air chamber of volume V has a neck area of cross section a into which a ball of mass m just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released , it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
View SolutionThe displacement of a simple harmonic oscillator is given by y=0.40sin(440t+0.61). For this, what are the value of amplitude.
View SolutionOn an average, a human heart is found to beat 75 times in a minute. Calculate its frequency and period.
View SolutionType of satellites are given in Column-I and their uses are given in Column-II. Match them properly :
Column-IColumn-II(1) Polar satellite(a) Tele communication(2) Geo-stationary satellite(b) Investigation(c) For information about atmosphere
View Solution.…. state of substance at very high temperature has generated hope of energy source for mankind.
View SolutionThe motion of a particle in S.H.M. is described by the displacement function, x=Acos(omegat+phi) , If the initial (t=0) position of the particle is 1cm and its initial velocity is omega cm s^(-1) , what are its amplitude and initial phase angle ? The angular frequency of the particle is pis^(-1) . If instead of the cosine function, we choos the sine function to describe the SHM : x=B sin(omegat+alpha) , what are the amlitude and intial phase of the particle with the above intial conditions ?
View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन निचे दिए गए विस्थापन फलन द्वारा किया जाता हैं, x(t)=Acos(ωt+ϕ) यदि कण की आरंभिक (t = 0) स्थिति 1 cm तथा उसकी आरंभिक वेग πcm s−1 हैं, तो कोण का आयाम तथा आरंभिक कला कोण क्या हैं ? कण की कोणीय आवृत्ति π s−1 हैं | यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या फलन चुनें x=Bsin(ωt+α) तो उपरोक्त आरंभिक प्रतिबंधों में कोण का आयाम तथा आरंभिक कला कोण क्या होगा ?
View SolutionA particle executing SHM is described by the displacement function x(t)=Acos(ωt+ϕ), if the initial (t=0) position of the particle is 1 cm, its initial velocity is πi cm s−1 and its angular frequency is πs−1, then the amplitude of its motion is
View SolutionA particle is SHM is described by the displacement function. x = A cos(omega t + phi), "where," omega = 2pi//T If the initial (t = 0) position of the particle is 1 cm and its initial velocity is pi cms^(-1) , what is the initial phase angle ? The angular frequency of the particle is pi s^(-1) .
View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया गया है,
x(t)=Acos(ωt+ϕ)
यदि कण की आरंभिक ( t = 0 ) स्थिति 1 सेमी तथा उसका आरंभिक वेग π सेमी/सेकण्ड है, तो कण का आयाम तथा आरंभिक कला कोण क्या है ? कण की कोणीय आवृत्ति π प्रति/सेकण्ड है | यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या ( cos ) फलन के स्थान पर हम ज्या ( sin ) फलन चुनें ,x=bsin(ω1+alphla), तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा ?
View Solutionसरल आवर्त गति करते हुए किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है -
x(t)=Acos(ωt+ϕ)
यदि कण की आरंभिक(t = 0) स्थिति 1 cm तथा उसका आरंभिक वेगπcm s−1 है , कण का आया तथा आरंभिक कला कौन क्या है ? कण की कोणीय आवृत्ति πs−1 है यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos ) फलन के स्थान पर हम ज्या(sin) फलन चुने x=Bsin(ωt+α) तो उपर्युक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला क्या होगा ?
View Solutionसरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिये गये विस्थापन फलन द्वारा किया जाता है,
x(t)=Acos(ωt+ϕ) यदि कण की आरंभिक (t=0) स्थिति 1 सेमी. तथा उसका आरम्भिक वेग π cm/s है, तो कण का आयाम तथा आरंभिक कला कोण क्या है? कण की कोणीय आवृत्ति π/s है। यदि सरल आवर्त गति का वर्णन करने के लिये कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फलन चुनें, x=Bsin(ωt+α) तो उपरोक्त आरंभिक प्रतिबंधों में कण का आयाम तथा आरंभिक कला कोण क्या होगा?
View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.
View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.
View SolutionThe motion of a particle executing simple harmonic motion is described by the displacement function,
x(t)=Acos(ωt+ϕ).
If the initial (t = 0) position of the particle is 1 cm and its initial velocity is ω cm/s, what are its amplitude and initial phase angle ? The angular frequency of the particle is πs−1. If instead of the cosine function, we choose the sine function to describe the SHM : x=Bsin(ωt+α), what are the amplitude and initial phase of the particle with the above initial conditions.
View Solution
