Question

Show that simple harmonic motion may be regarded as the projection of uniform circular motion along a diameter of the circle.

Explanation

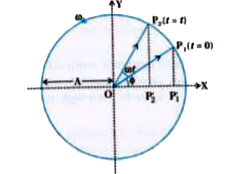
Suppose as shown in figure, a particle is moving with a constant angular speed `omega` in an inti-clockwise direction on a circular path having centre O and radius A.
At time t=0, particle at position `P_(1)` and its position vector `vec(OP_1)` makes an angle `phi` with positive X-axis.
Projection of `OP_(1)` on X-axis is `OP._(1)`
At time t=t, particle displaced by angular displacement `omega t`, it reaches at point `P_(2)` and its position vector `vec(OP_2)` makes an angle `omega t+ phi` with X-axis.
Projection of position vector `OP_(2)` on X-axis is `OP._(2)`.
As the particle P moving on a circle, its point of perpendicular on X-axis is given by `x(t)= A cos (omega t+ phi)`. It is the X-component of position vector at any time.
This equation is the general equation of SHM.
From this it is said that the projection of uniform circular motion on a diameter of the reference circle is SHM.
The particle moving on uniform circular path is called reference particle and the circular path of reference particle is reference circle.
If the projection of reference particle taken on Y-axis, the displacement of particle on Y-axis is `y(t)= A sin (omega t+ phi)`.