Derive equation for heat flow rate in rectangular block of solid. Solution in Gujrati
Figure shows a rectangular block of solid of cross section .A..
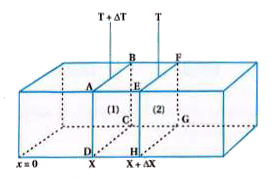
Let us consider two cross sections ABCD and EFGH, at a distance x and Δx from one end of a block having temperature T+ΔT and T respectively.
Here, the distance between two cross section is Δx and temperature difference is ΔT.
The ratio ΔT/Δx is called temperature gradient
Temperature gradient : The difference in temperature per unit distance between two parts of a solid is called distance between two parts of a solid is called as temperature gradient parts of a solid is called as temperature gradient. Its unit is Kelvin/meter and dimensional formula is M0L−1T0K1.
Experiment shown that for a small change in temperature, the amount of heat passing between these two cross sectional planes in direction perpendicular to these planes in time Δt depends on the following factors :
ΔQ∝ΔTΔx (For given Δt and A)
ΔQ∝Δt (For given ΔT/Δx and A)
ΔQ∝A For given Δt and ΔT/Δx)
∴ΔQ=−kAΔTΔxΔt
ΔQΔt=−kAΔTΔx . . .(1)
Here, k is constant of proportionality called thermal conductivity of the material of the block. Its value depends on the type of the material and to some extent on the temperature.
The materials with higher value of thermal consuctivity are good conductors of heat.
Normalally, if the differnces in the temperatures of different parts of solid are not very large, k can be considered a constant.
Negative sign in above equation indicates that with the increase in x the temperature decreases.
Taking limits Δx→0 and Δt→0 in equation (1)
dQdt=−kAdTdx . . . (2)
∴H=−kadQdt
dQdt=H is called heat current. Heat current is the rate of flow of heat through any cross section.
Its unit is cal/s or J/s, its dimensional formula is M1L2T−3.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Section - B (Numericals) Numerical From Textual Illustration
Explore 8 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Section - B
Explore 10 Videos
- THERMAL PROPERTIES OF MATTERBook:KUMAR PRAKASHANChapter:THERMAL PROPERTIES OF MATTERExercise:Try Yourself (VSQs)
Explore 84 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:KUMAR PRAKASHANChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SECTION-F (SECTION-D) QUESTIONS PAPER
Explore 1 Video
- THERMODYANMICS Book:KUMAR PRAKASHANChapter:THERMODYANMICS Exercise:Question Paper
Explore 11 Videos
Similar Questions
Show that the coefficient of area expansions, (ΔA/A)/ΔT, of a rectangular sheet of the solid is twice its linear expansively, αl.(αl=10−5K−1)
View SolutionShow that the coefficient of area expansions, (ΔA/A)/ΔT, of a rectangular sheet of the solid is twice its linear expansively, αl.(αl=10−5K−1)
View Solution''Amount of heat is greater in hot body than cold body''. Check correctness of this statement.
View SolutionA rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
View SolutionWhy is a steam burn more damaging than a burn with boiling water of the same ?
View SolutionRate Of Heat Flow
View SolutionThe rate of flow of heat per unit area per unit temperature gradient across the solid is called………..
View SolutionIf the end of metal rod is heated then the rate of flow the heat does not depend on
View SolutionIn variable state, the rate of flow of heat is controlled by
View Solutionऊष्मा चालन की स्थायी अवस्था से क्या तात्पर्य है? स्थायी अवस्था में ऊष्मा प्रवाह की दर की समीकरण की सहायता से ऊष्मा-चालकता गुणांक की परिभाषा दीजिए एवं मात्रक ज्ञात कीजिए।
View Solutionकिसी धात्वीय छड़ में, ऊष्मा चालन की स्थायी अवस्था से क्या अभिप्राय है ? स्थायी अवस्था में ऊष्मा प्रवाह की दर का समीकरण लिखकर ऊष्मा चालकता गुणांक की परिभाषा तथा विमीय सूत्र निकालिये |
View Solutionस्थायी अवस्था में ऊष्मा प्रवाह की दर निर्भर करती है :
View SolutionJoule law of heating is ___________.
View SolutionIn Q.No.4-49, the lowest rate of flow of heat is for:
View SolutionWhat is venturi-meter? Derive an expression for the rate of flow of a liquid using this device.
View Solution