If the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is
a+b
√a+b
a×b
a√b
The correct Answer is:B
Step by step video, text & image solution for If the angles of elevation of the top of a tower from two points at distances a and b from the base and in the same straight line with it are complementary then the height of the tower is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEIGHTS AND DISTANCES Book:MCGROW HILL PUBLICATIONChapter:HEIGHTS AND DISTANCES Exercise:MULTIPLE CHOICE QUESTIONS
Explore 41 Videos
- FUNDAMENTALS OF ALGEBRABook:MCGROW HILL PUBLICATIONChapter:FUNDAMENTALS OF ALGEBRAExercise:Multiple Choice Questions
Explore 23 Videos
- INCOMPLETE FIGURES Book:MCGROW HILL PUBLICATIONChapter:INCOMPLETE FIGURES Exercise:EXAMPLE
Explore 2 Videos
Similar Questions
The angles of elevation of the top of a tower from two points at distances a and b metres from the base and in the same straight line with it are complementary. Prove that the height of the tower is √ab metres.
View SolutionIf the angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary, find the height of the tower.
View Solution
Knowledge Check
The angles of elevation of the top of a tower from two points on the ground at distances 32 m and 18 m from its base and in the same straight line with it are complementary. The height(in m) of the tower is .....
A24B20C28D16The angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is
A5mB15mC5√2mD75m
The angles of elevation of the top of a tower from two points situated at distances 36m and 64m from its base and in the same straight line with it are complementary. What is the heigth of the tower
View SolutionIf the angles of elevation of a tower from two points distant a and b from the base and in the same straight line with it are complementary, then the height of the tower is ab (b) √ab (c) ab (d) √ab
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.
View SolutionThe angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
View SolutionThe angles of elevatio of the top of a tower from two points 8 m and 32 m from the base and in the same straight line with it are complementary. Find the heigt of the tower.
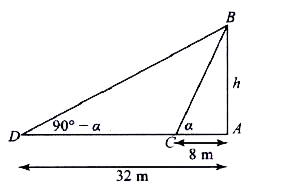
View SolutionThe angles of elevation of the top of a tower from two points which are at distances of 10 m and 5 m from the base of the tower and in the same straight line with it are complementary. The height of the tower is :
View Solution
