1 Vm−1 equals
1N
1Nm−1
1Nc−1
1JC
The correct Answer is:A
To solve the question "1 Vm^(-1) equals," we need to understand the units involved and their relationships.
1. Understanding the Unit:
- The unit "Vm^(-1)" stands for "volt per meter." This is a unit of electric field strength.
2. Definition of Electric Field:
- The electric field (E) is defined as the force (F) experienced by a unit charge (Q) placed in the field. Mathematically, this is expressed as:
E=FQ
3. Relating Electric Field to Voltage:
- The electric field can also be defined in terms of electric potential (V) and distance (d):
E=−dVdx
- In a uniform electric field, this simplifies to:
E=Vd
- Where V is the voltage and d is the distance over which the potential changes.
4. Unit Conversion:
- From the definition of electric field, we can express it in terms of force and charge:
E=FQ
- The SI unit of force (F) is Newton (N), and the SI unit of charge (Q) is Coulomb (C).
- Therefore, the unit of electric field can also be expressed as:
E=NewtonCoulomb=N/C
5. Equating Units:
- Now, we can equate the units:
1 Vm−1=1 N/C
- This means that 1 volt per meter is equivalent to 1 Newton per Coulomb.
6. Final Expression:
- Thus, we can conclude:
1 Vm−1=1 N/C=1 Newton per Coulomb
Final Answer:
1 Vm^(-1) equals 1 Newton per Coulomb (1 N/C).
- The unit "Vm^(-1)" stands for "volt per meter." This is a unit of electric field strength.
- The electric field (E) is defined as the force (F) experienced by a unit charge (Q) placed in the field. Mathematically, this is expressed as:
E=FQ
- The electric field can also be defined in terms of electric potential (V) and distance (d):
E=−dVdx
- In a uniform electric field, this simplifies to:
E=Vd
- Where V is the voltage and d is the distance over which the potential changes.
- From the definition of electric field, we can express it in terms of force and charge:
E=FQ
- The SI unit of force (F) is Newton (N), and the SI unit of charge (Q) is Coulomb (C).
- Therefore, the unit of electric field can also be expressed as:
E=NewtonCoulomb=N/C
- Now, we can equate the units:
1 Vm−1=1 N/C
- This means that 1 volt per meter is equivalent to 1 Newton per Coulomb.
- Thus, we can conclude:
1 Vm−1=1 N/C=1 Newton per Coulomb
1 Vm^(-1) equals 1 Newton per Coulomb (1 N/C).
Topper's Solved these Questions
- MISCELLANEOUS QUESTIONSBook:MCGROW HILL PUBLICATIONChapter:MISCELLANEOUS QUESTIONSExercise:PART-B
Explore 99 Videos
- MEASUREMENTBook:MCGROW HILL PUBLICATIONChapter:MEASUREMENTExercise:ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
Explore 13 Videos
- MOTIONBook:MCGROW HILL PUBLICATIONChapter:MOTIONExercise:HIGHER ORDER THINKING QUESTIONS
Explore 48 Videos
Similar Questions
Knowledge Check
[1−2(1−2)−1]−1
A13B−13C−1D12In an electromagnetic wave, the maximum value of the electric field is 100Vm−1 The average intensity is [ε90)=8.8×10−12c−2N−1m2]
A13.2 W m−2B36.5 W m−2C46.7 W m−2D765 W m−2In a figure shown the electric field intenisity at r=1,r=6m,r=9m and Vm−1 is
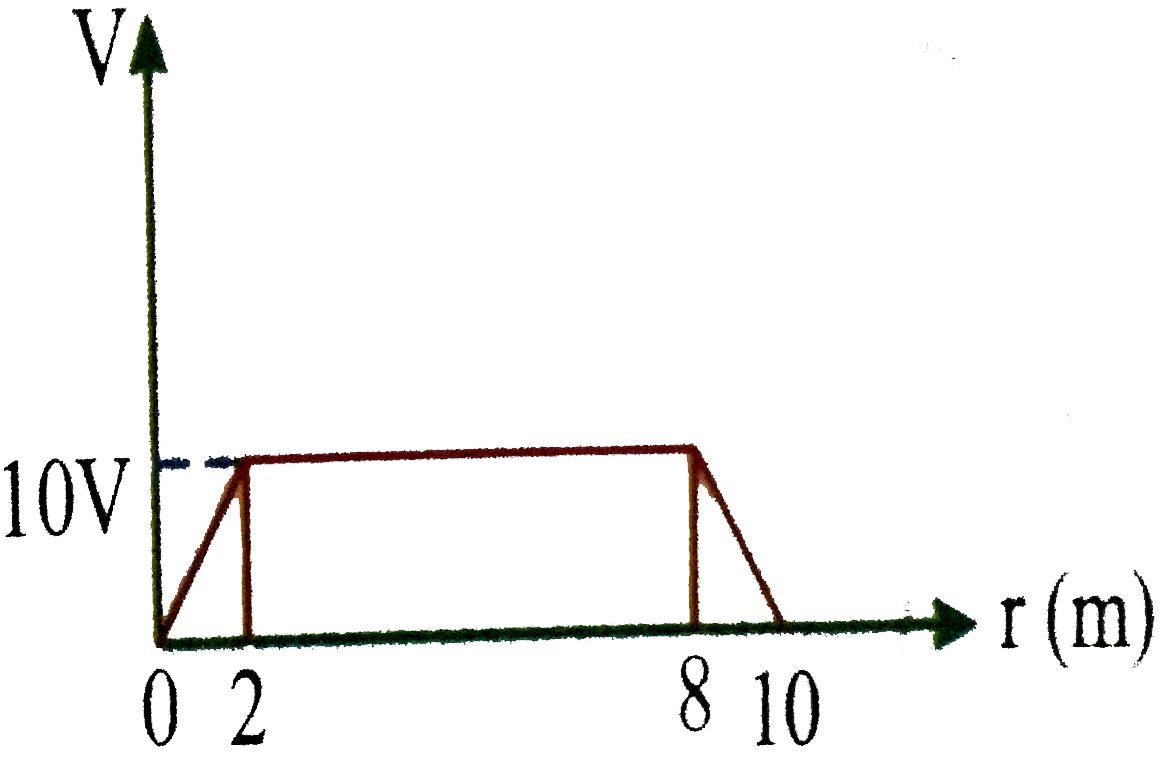 A−5,−1.67,+5B−5,0,+5C0,1.67,0D+5,1.67,−5
A−5,−1.67,+5B−5,0,+5C0,1.67,0D+5,1.67,−5
{(13)−1−(14)−1}−1is equal to.
View SolutionWhat is 1am−n−1+1an−m−1 equal to ?
View Solution11+an−m + 11+am−n
View SolutionIn an electromagnetic wave, the electric and magnetising fields are 100 Vm−1 and 0.265 Am−1. The maximum energy flow is
View SolutionIn an experiment the electric field was found to oscillate with an amplitude of 18Vm−1. The amplitude of oscillations of the magnetic field will be
View Solution