A force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest
f1 may be equal to f2
f1must not be equal to f2
f1and f2 must be zero
f1 must be equal to f2
The correct Answer is:A
According to condition of motion under two forces, f1 and f2 must be acting in opposite directions and may be equal, not necessarily must be equal.
Topper's Solved these Questions
- MISCELLANEOUS QUESTIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - MISCELLANEOUS QUESTIONSEXERCISE - PART-B
99 Videos
- MEASUREMENTBOOK - MCGROW HILL PUBLICATIONCHAPTER - MEASUREMENTEXERCISE - ELEMENTARY QUESTIONS (HIGHER ORDER THINKING QUESTIONS)
13 Videos
- MOTIONBOOK - MCGROW HILL PUBLICATIONCHAPTER - MOTIONEXERCISE - HIGHER ORDER THINKING QUESTIONS
48 Videos
Similar Questions
A time dependent force F=3t^(2)+6t acts on a particle of mass 18kg .If particle starts from rest the work done by the force during the first 3 second will be :
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
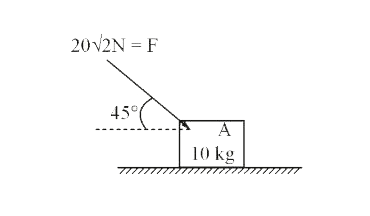
View Solution
Knowledge Check
A time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
A9JB18JC4.5JD22JWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
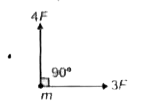 AaB2aC5aD8a
AaB2aC5aD8aWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
A→F1/mB→F1/mC→F2−→F3/mD→F2/m
When a force F1 acts on a particle, frequency is 6 Hz and when a force F2 acts, frequency is 8 Hz. What is the frequency when both the forces act simultaneously in the same direction?
View SolutionGiven four forces : →F1=3ˆi−ˆj+9ˆk →F2=2ˆi−2ˆj+16ˆk →F3=9ˆi+ˆj+18ˆk →F4=ˆi+2ˆj−18ˆk If all these forces act on a particle at rest at the origin of a coordinate system, then identify the plane in which the particle would begin to move ?
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
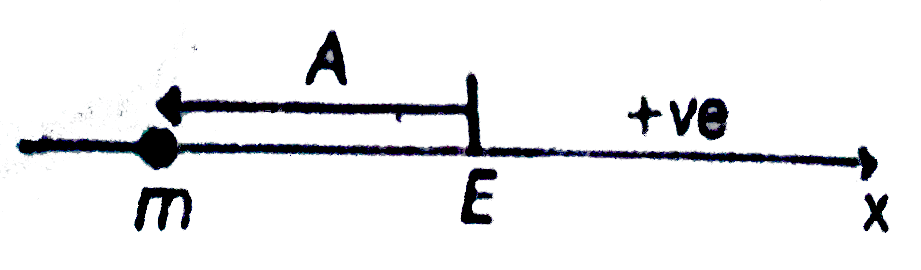
View SolutionForces acting on a particle moving in a straight line varies with the velocity of the particle as F=αυ where α is constant. The work done by this force in time interval Δt is :
View Solution
