Which of the following shows the bending of light from rarer (R) into denser (D) medium?
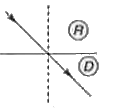

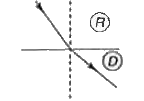
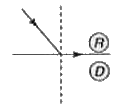
The correct Answer is:B
To determine which of the given options shows the bending of light from a rarer medium (R) into a denser medium (D), we can follow these steps:
1. Understand the Concept of Refraction:
When light travels from a rarer medium to a denser medium, it bends towards the normal. The refractive index (μ) of the rarer medium is less than that of the denser medium.
2. Identify the Relationship Between Angles:
According to Snell's Law, the relationship can be expressed as:
μrsin(i)=μdsin(r)
where:
- μr = refractive index of the rarer medium
- μd = refractive index of the denser medium
- i = angle of incidence
- r = angle of refraction
3. Analyze the Values of Refractive Indices:
Since the refractive index of the rarer medium is less than that of the denser medium, we have:
μd>μr
This implies that the term μdμr>1.
4. Determine the Relationship Between Angles:
From Snell's Law rearranged, we can derive:
sin(r)=μrμdsin(i)
Since μrμd<1, it follows that:
sin(r)<sin(i)
This indicates that the angle of refraction r is less than the angle of incidence i:
r<i
5. Conclusion About the Direction of Bending:
Since r<i, the ray of light bends towards the normal when it enters the denser medium from the rarer medium.
6. Evaluate the Given Options:
- Option 1: Light travels straight - Incorrect.
- Option 2: Light bends towards the normal (i > r) - Correct.
- Option 3: Light bends outward (r > i) - Incorrect.
- Option 4: Light bends excessively along the interface (r = 90°) - Incorrect.
7. Final Answer:
The correct option that shows the bending of light from a rarer medium into a denser medium is Option 2.
When light travels from a rarer medium to a denser medium, it bends towards the normal. The refractive index (μ) of the rarer medium is less than that of the denser medium.
According to Snell's Law, the relationship can be expressed as:
μrsin(i)=μdsin(r)
where:
- μr = refractive index of the rarer medium
- μd = refractive index of the denser medium
- i = angle of incidence
- r = angle of refraction
Since the refractive index of the rarer medium is less than that of the denser medium, we have:
μd>μr
This implies that the term μdμr>1.
From Snell's Law rearranged, we can derive:
sin(r)=μrμdsin(i)
Since μrμd<1, it follows that:
sin(r)<sin(i)
This indicates that the angle of refraction r is less than the angle of incidence i:
r<i
Since r<i, the ray of light bends towards the normal when it enters the denser medium from the rarer medium.
- Option 1: Light travels straight - Incorrect.
- Option 2: Light bends towards the normal (i > r) - Correct.
- Option 3: Light bends outward (r > i) - Incorrect.
- Option 4: Light bends excessively along the interface (r = 90°) - Incorrect.
The correct option that shows the bending of light from a rarer medium into a denser medium is Option 2.
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:MCGROW HILL PUBLICATIONChapter:REFRACTION OF LIGHTExercise:HIGHER ORDER THINKING QUESTIONS
Explore 37 Videos
- REFLECTION OF LIGHT Book:MCGROW HILL PUBLICATIONChapter:REFLECTION OF LIGHT Exercise:HIGHER ORDER THINKING QUESTIONS
Explore 10 Videos
- SOURCES OF ENERGY Book:MCGROW HILL PUBLICATIONChapter:SOURCES OF ENERGY Exercise:ELEMENTARY QUESTIONS
Explore 82 Videos
Similar Questions
Knowledge Check
Which of the following shows the bending of light from denser (D) medium into a rarer (R) medium?
A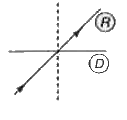 B
B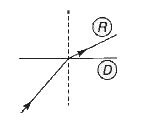 C
C D
D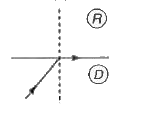
Which of the following diagrams shows the bending of light from a denser medium into a rarer medium?
A B
B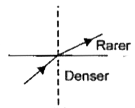 C
C D
D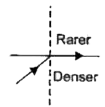
Bending of light rays in denser medium is termed as:
AReflectionBDispersionCRefractionDDeflection
Can total internal reflection occur when light goes from a rarer to a denser medium.
View SolutionCan total internal reflection occur when light goes from a rarer to a denser medium.
View SolutionHow do the frequency and wavelength of light change when it goes from a rarer to a denser medium ?
View SolutionBending of light rays in denser medium is termed as:
View SolutionWhen light travels from a rarer medium to a denser medium, it ________
View Solution