The graph between L and Tis correctly shown by (Fig. 7.2)
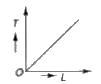
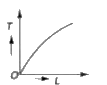
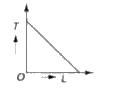

The correct Answer is:B
To solve the question regarding the graph between the length (L) of a simple pendulum and its time period (T), we can follow these steps:
1. Understand the Relationship: The time period T of a simple pendulum is given by the formula:
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
2. Identify the Proportionality: From the formula, we can deduce that:
T∝√L
This means that the time period T is directly proportional to the square root of the length L.
3. Square the Relationship: To express this relationship in a more graph-friendly format, we can square both sides:
T2∝L
This indicates that if we plot T2 against L, we should get a straight line.
4. Graphical Representation: Since T2 is proportional to L, the graph of T2 (on the y-axis) versus L (on the x-axis) will be a straight line passing through the origin.
5. Identifying the Correct Option: Based on the options provided in the question, we need to look for a graph that shows a parabolic curve when plotting T against L. Since T is proportional to √L, the graph of T versus L will be a curve that rises as L increases, but it will not be a straight line.
6. Conclusion: The correct graph will show that as the length L increases, the time period T also increases, and the relationship is not linear but rather follows a parabolic shape.
Final Answer:
The correct graph between L and T is the one that shows a curve indicating that T increases with increasing L, specifically a parabolic curve.
T=2π√Lg
where L is the length of the pendulum and g is the acceleration due to gravity.
T∝√L
This means that the time period T is directly proportional to the square root of the length L.
T2∝L
This indicates that if we plot T2 against L, we should get a straight line.
The correct graph between L and T is the one that shows a curve indicating that T increases with increasing L, specifically a parabolic curve.
Topper's Solved these Questions
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - WAVE MOTION AND SOUND EXERCISE - HIGH ORDER THINKING QUESTIONS22videos
WAVE MOTION AND SOUND
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS82videos
SOURCES OF ENERGY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING QUESTIONS29videos
WORK AND ENERGY
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph between L and T is correctly shown by
A B
B C
C D
D
- Question 2 - Select One
The graph between L and T2 is
A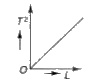 B
B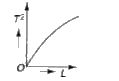 C
C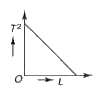 D
D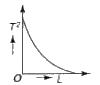
- Question 3 - Select One
The graph between L and T2 is
A B
B C
C D
D
Angular momentum L is given by L=Pr The variation of log L and logP is correctly shown in Fig.
View SolutionIn the circuit shown in Fig. 7.45,
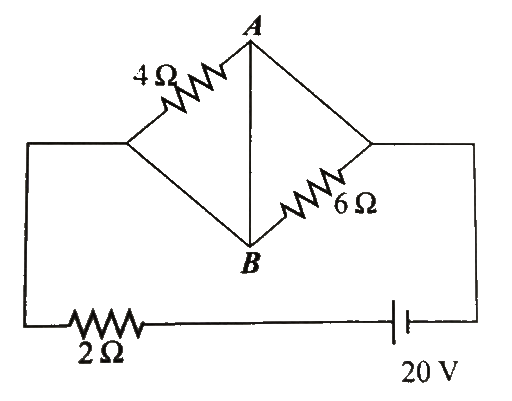 View Solution
View SolutionThe x−t graph of particle moving along a straight line is shown in figure
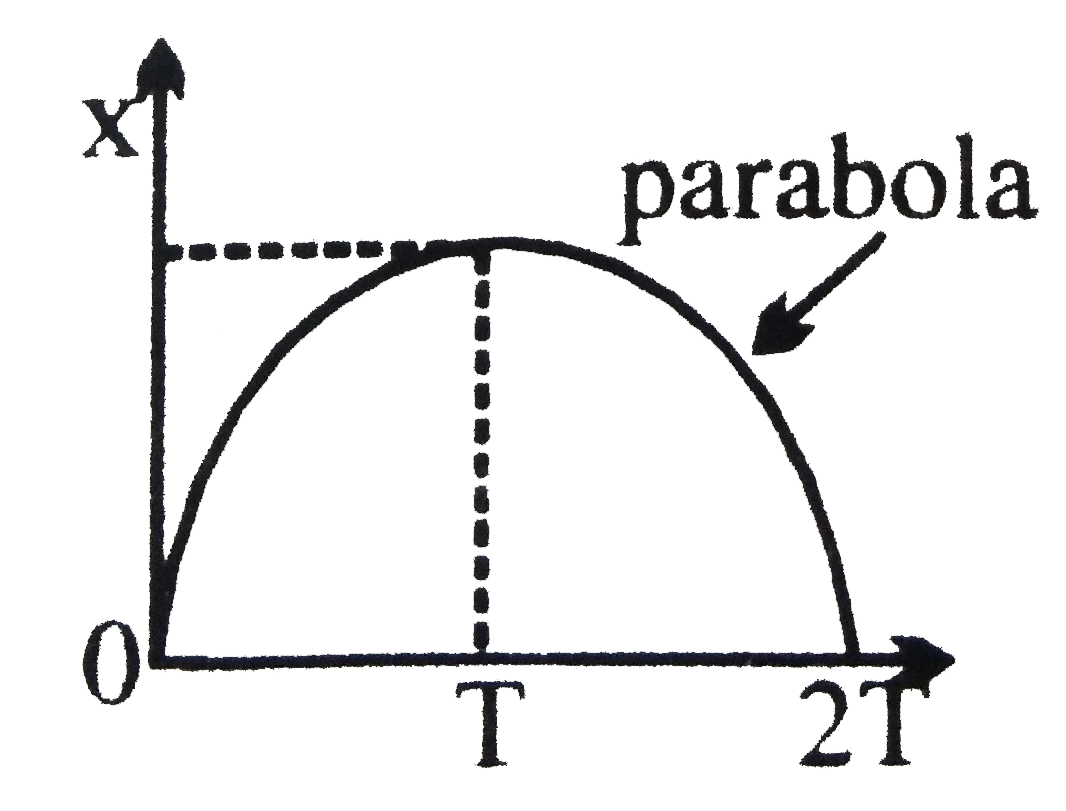
The a−t graph of the particle is correctly shown byView SolutionThe x-t graph of a particle moving along a straight line is shown in figure
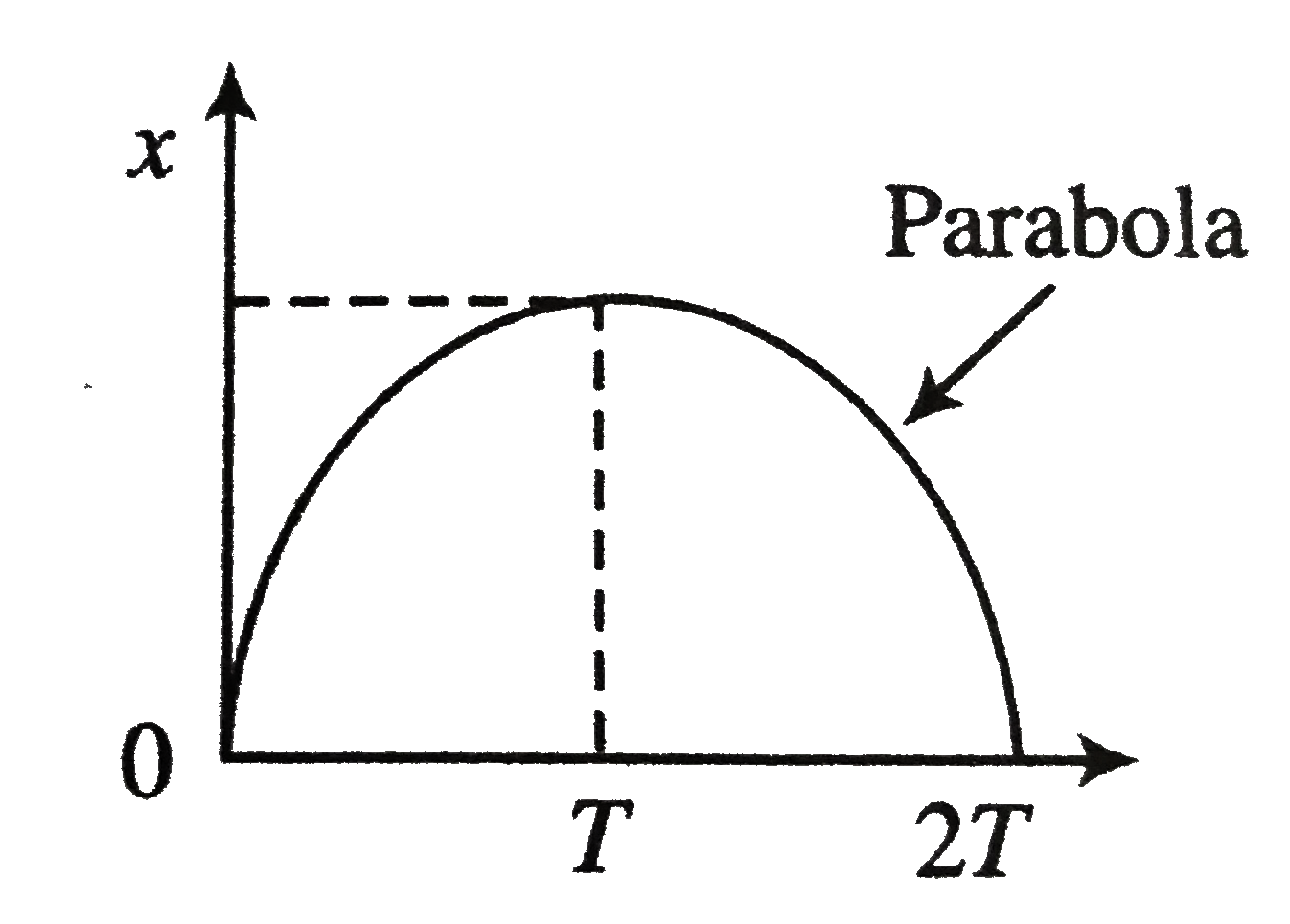
The v-t graph of the particle is correctly shown byView SolutionThe x-t graph of a particle moving along a straight line is shown in figure
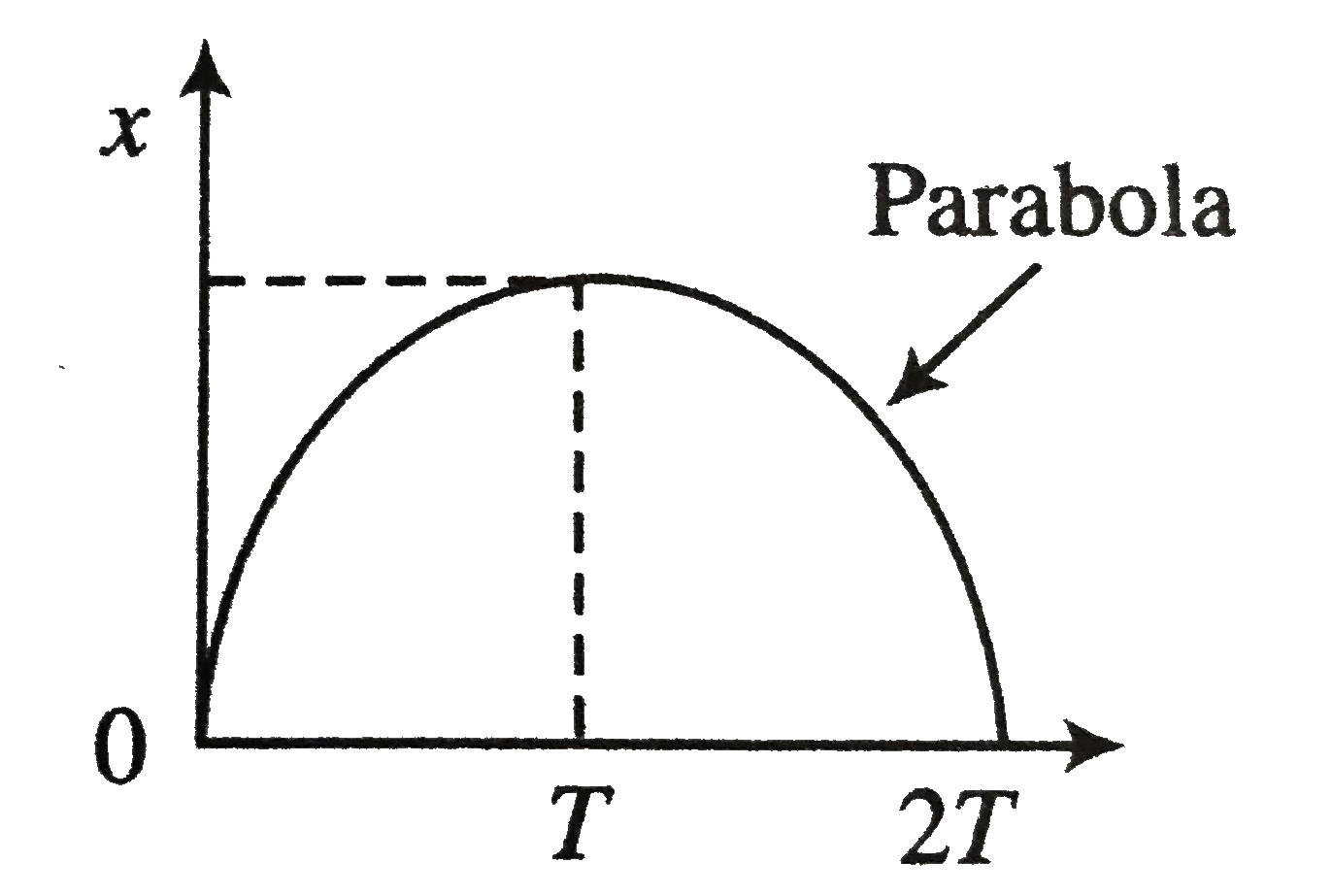
The a-t graph of the particle is correctly shown byView Solution
