A stone of mass 1 kg falls to the earth from a height of 10 m. The kinetic energy of the stone when it is 4 m above the ground is
58.8 J
5.88 J
588 J
none of these
The correct Answer is:A
To find the kinetic energy of a stone of mass 1 kg when it is 4 m above the ground after falling from a height of 10 m, we can use the principle of conservation of mechanical energy. Here’s the step-by-step solution:
Step 1: Identify the initial and final heights
- The initial height (H1) from which the stone falls is 10 m.
- The final height (H2) when we want to find the kinetic energy is 4 m.
Step 2: Calculate the potential energy at the initial height
The potential energy (PE) at height H1 can be calculated using the formula:
PE=mgh
Where:
- m=1kg (mass of the stone)
- g=9.8m/s2 (acceleration due to gravity)
- h=H1=10m
Calculating the potential energy:
PEinitial=1×9.8×10=98J
Step 3: Calculate the potential energy at the final height
Now, we calculate the potential energy at height H2 (4 m):
PEfinal=mgh
Where:
- h=H2=4m
Calculating the potential energy:
PEfinal=1×9.8×4=39.2J
Step 4: Apply the conservation of mechanical energy
According to the conservation of mechanical energy:
PEinitial+KEinitial=PEfinal+KEfinal
Since the stone is initially at rest, the initial kinetic energy (KE_initial) is 0:
98J+0=39.2J+KEfinal
Step 5: Solve for the final kinetic energy
Rearranging the equation to find KEfinal:
KEfinal=PEinitial−PEfinal
Substituting the values:
KEfinal=98J−39.2J=58.8J
Final Answer
The kinetic energy of the stone when it is 4 m above the ground is 58.8 Joules.
---
- The initial height (H1) from which the stone falls is 10 m.
- The final height (H2) when we want to find the kinetic energy is 4 m.
The potential energy (PE) at height H1 can be calculated using the formula:
PE=mgh
Where:
- m=1kg (mass of the stone)
- g=9.8m/s2 (acceleration due to gravity)
- h=H1=10m
PEinitial=1×9.8×10=98J
Now, we calculate the potential energy at height H2 (4 m):
PEfinal=mgh
Where:
- h=H2=4m
PEfinal=1×9.8×4=39.2J
According to the conservation of mechanical energy:
PEinitial+KEinitial=PEfinal+KEfinal
Since the stone is initially at rest, the initial kinetic energy (KE_initial) is 0:
98J+0=39.2J+KEfinal
Rearranging the equation to find KEfinal:
KEfinal=PEinitial−PEfinal
Substituting the values:
KEfinal=98J−39.2J=58.8J
The kinetic energy of the stone when it is 4 m above the ground is 58.8 Joules.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A body of mass 2 kg is dropped from a height of 1 m. It s kinetic as it reaches the ground is
A19.6 JB19.6 NC19.6 kgD19.6 mA steel ball of mass 0.1 kg falls freely from a height of 10 m and bounces to a height of 5.4 m from the ground. If the dissipated energy in this process is absorbed by the ball, the rise in its temperature is (specific heat of steel =460K/kg∘/C,g=10m/s2)
A0.01∘CB0.1∘CC1∘CD1.1∘CA stone of mass 2 kg is projected upward with kinetic energy of 98 J. The height at which the kinetic energy of the stone becomes half its original value, is given by
A5 mB2.5 mC1.5 mD0.5 m
A body A of mass 3 . 0 kg and a body B of mass 10 kg are dropped simultaneously from a height of 14 . 9 m Calculate
their kinetic energies when they are 10 m above the ground
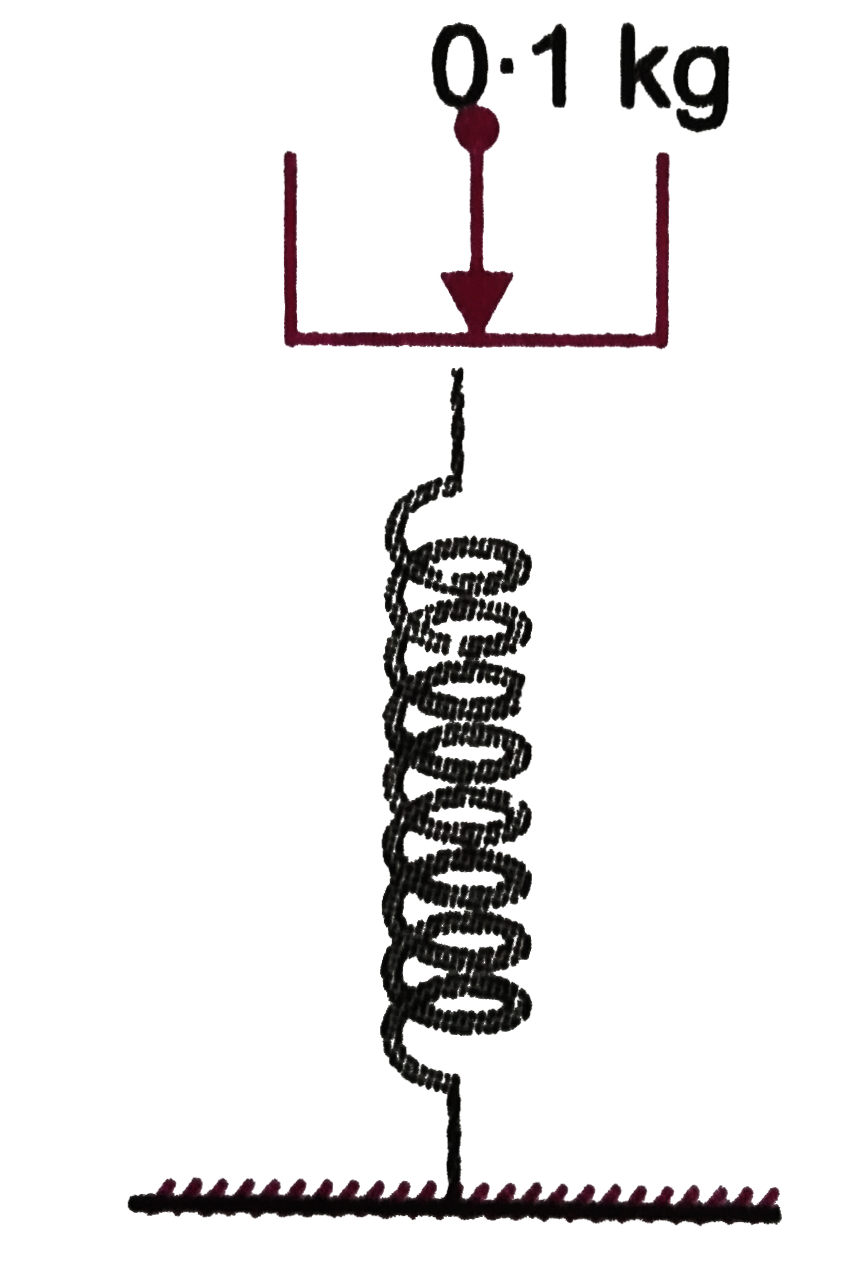
View SolutionA massless platform is kept on a light elastic spring as shown in figure. When a small stone of mass 0.1 kg is dropped on the pan from a height of 0.24 m, the spring compresses by 0.01m. From what height should the stone be droppped to cause a compression of 0.04m in the spring ?
View SolutionA stone is thrown upwards and it rises to a height 0f 200m. The relative velocity of the stone with respect to the earth will be maximum at :-
View SolutionIn a shotput event an athlete throws the shotput of mass 20 kg with an initial speed of 2ms−1 at 45∘ from height 3 m above ground. Assuming air resistance to be negligible and acceleration due to gravity to be 10ms−2, the kinetic energy of the shotput when it just reaches the ground will be
View SolutionIn a shotput event an athlete throws the shotput of mass 10kgwith an initial speed of 1ms−1 at 45∘ from a height 1.5m above ground. Assuming air resistance to be negligible and acceleration due to gravity to be 10ms−2, the kinetic energy of the shotput when it just reaches the ground will be
View Solution

