the correct variation between √E and p is shown by
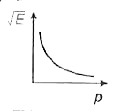
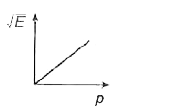

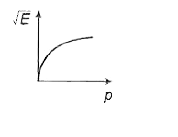
The correct Answer is:B
To solve the question regarding the correct variation between √E (where E is kinetic energy) and p (momentum), we can follow these steps:
1. Understand the Definitions:
- Kinetic Energy (E) is given by the formula:
E=12mv2
- Momentum (p) is defined as:
p=mv
2. Express Velocity in Terms of Momentum:
- From the momentum equation, we can express velocity v as:
v=pm
3. Substitute Velocity into Kinetic Energy Formula:
- Substitute v into the kinetic energy formula:
E=12m(pm)2
- Simplifying this gives:
E=12m⋅p2m2=p22m
4. Relate Kinetic Energy to Momentum:
- Rearranging the equation, we have:
p2=2mE
- Taking the square root of both sides gives:
p=√2mE
5. Express the Relationship:
- This shows that momentum p is directly proportional to √E:
p∝√E
6. Graphical Representation:
- If we plot p on the y-axis and √E on the x-axis, the relationship will be linear, indicating that as momentum increases, the square root of kinetic energy also increases proportionally.
7. Conclusion:
- Therefore, the correct variation between √E and p is a straight line graph, confirming that p is directly proportional to √E.
- Kinetic Energy (E) is given by the formula:
E=12mv2
- Momentum (p) is defined as:
p=mv
- From the momentum equation, we can express velocity v as:
v=pm
- Substitute v into the kinetic energy formula:
E=12m(pm)2
- Simplifying this gives:
E=12m⋅p2m2=p22m
- Rearranging the equation, we have:
p2=2mE
- Taking the square root of both sides gives:
p=√2mE
- This shows that momentum p is directly proportional to √E:
p∝√E
- If we plot p on the y-axis and √E on the x-axis, the relationship will be linear, indicating that as momentum increases, the square root of kinetic energy also increases proportionally.
- Therefore, the correct variation between √E and p is a straight line graph, confirming that p is directly proportional to √E.
Topper's Solved these Questions
Similar Questions
The variate x and u are related by u=x−ah then correct relation between σx and σu is
View SolutionFigure (b) shows the variation of pressure (p) with depth (h) along a vertical wall supporting two liquids of different densities as shown in Fig. (a). Identify the correct variation of pressure in the liquid of density ρ2.

View Solution
Knowledge Check
In question 62, the correct variation between √Eand1√p is shown by
A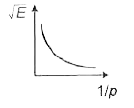 B
B C
C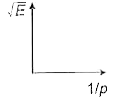 D
D
The binding energies of the atom of elements P and Q are EP and EQ respectively. There atoms of element Q fuse on atom of element P. The correct relation between EP,EQ and e will be
AEQ=3EP+eBEQ=3EP−eCEP=3EQ+eDEP=3EQ−eThe nuclear binding energies of the elements P and Q are EP and EQ respectively. Three nuclei of elements Q fuse to form one nucleus of element P. In this process the energy released is 'e'. The correct relation between EP,EQ and e will be
AEQ=3EP+eBEQ=3EP−eCEP=3EQ+eDEP=3EQ−e
If p and E represent linear momentum and kinetic energy respectively, then the graph between E and pis correctly shown by
View SolutionIf for a given substance, melting point is TB and freezing point is TA then correct variation of entropy is by graph between entropy change and temperature is
View SolutionWhich of the following shown the correct relationship between the pressure 'P' and density ρ of an idealgas at constant tem pera ture?
View SolutionWhich one of the following correctly represents the variation between linear momentum (P) and kinetic energy (E) ofa body?
View SolutionThe graph between the current and the time for an inductance coil is shown below. Which of the following graph show the voltage-time variation-

View Solution
