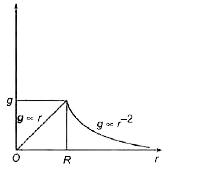
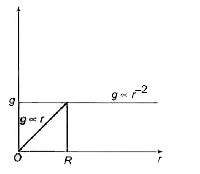
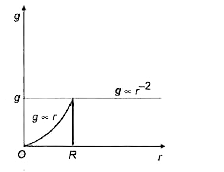
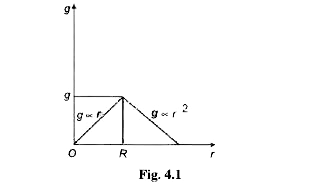
The variation of g with height or depth (r ) is shown correctly by the graph in Fig .4.2 (where R is radius of the earth),
The correct Answer is:A
To analyze the variation of gravitational acceleration (g) with height and depth, we can break down the problem into several steps:
Step 1: Understanding the Regions
1. Above the Surface of the Earth: When we are at a height above the Earth's surface, the distance from the center of the Earth (r) is greater than the Earth's radius (R).
- Here, g decreases as r increases.
- The formula for gravitational acceleration at height h above the surface is given by:
g=GMr2
- Since r=R+h, as h increases, g decreases.
Step 2: At the Surface of the Earth
2. On the Surface of the Earth: At the surface, r=R.
- The gravitational acceleration is maximum and is given by:
g=GMR2
- This is the point where g has its highest value, approximately 9.8m/s2.
Step 3: Inside the Earth
3. Below the Surface of the Earth: When we are at a depth d inside the Earth, the distance from the center of the Earth (r) is less than the Earth's radius (R).
- The formula for gravitational acceleration at a depth d is:
g=GMR3⋅r
- Here, r is the distance from the center of the Earth, which decreases as we go deeper. Thus, g decreases linearly with depth until it reaches zero at the center of the Earth.
Step 4: Graphing the Variation
4. Graphing:
- On the graph, the x-axis represents the distance from the center of the Earth (r), while the y-axis represents the gravitational acceleration (g).
- For r<R (inside the Earth): The graph is a straight line increasing from (0,0) to (R, g_max).
- At r=R (on the surface): The graph reaches its maximum value g=GMR2.
- For r>R (above the surface): The graph curves downward, showing that g decreases as r increases.
Conclusion
From the analysis, we can conclude that:
- As we move from the center of the Earth to the surface, g increases.
- At the surface, g is maximum.
- As we move above the surface, g decreases.
1. Above the Surface of the Earth: When we are at a height above the Earth's surface, the distance from the center of the Earth (r) is greater than the Earth's radius (R).
- Here, g decreases as r increases.
- The formula for gravitational acceleration at height h above the surface is given by:
g=GMr2
- Since r=R+h, as h increases, g decreases.
2. On the Surface of the Earth: At the surface, r=R.
- The gravitational acceleration is maximum and is given by:
g=GMR2
- This is the point where g has its highest value, approximately 9.8m/s2.
3. Below the Surface of the Earth: When we are at a depth d inside the Earth, the distance from the center of the Earth (r) is less than the Earth's radius (R).
- The formula for gravitational acceleration at a depth d is:
g=GMR3⋅r
- Here, r is the distance from the center of the Earth, which decreases as we go deeper. Thus, g decreases linearly with depth until it reaches zero at the center of the Earth.
4. Graphing:
- On the graph, the x-axis represents the distance from the center of the Earth (r), while the y-axis represents the gravitational acceleration (g).
- For r<R (inside the Earth): The graph is a straight line increasing from (0,0) to (R, g_max).
- At r=R (on the surface): The graph reaches its maximum value g=GMR2.
- For r>R (above the surface): The graph curves downward, showing that g decreases as r increases.
From the analysis, we can conclude that:
- As we move from the center of the Earth to the surface, g increases.
- At the surface, g is maximum.
- As we move above the surface, g decreases.
Topper's Solved these Questions
- GRAVITATION Book:MCGROW HILL PUBLICATIONChapter:GRAVITATION Exercise:HIGHER ORDER THINKING QUESTIONS
Explore 25 Videos
- ELECTRIC CURRENT Book:MCGROW HILL PUBLICATIONChapter:ELECTRIC CURRENT Exercise:HIGHER ORDER THINKING QUESTIONS
Explore 29 Videos
- HEATBook:MCGROW HILL PUBLICATIONChapter:HEATExercise:HIGHER ORDER THINKING QUESTIONS
Explore 15 Videos
Similar Questions
Discuss the variation of g with height and depth.
View SolutionObtain an expression for the acceleration due to gravity on the surface of the earth in terms of mass of the earth and its radius. Discuss the variation of acceleration due to gravity with altitude and depth. If a body is taken to a height R / 4 from the surface of the earth, find percentage decrease in the weight of the body ? Here R is the radius of the earth.
View Solution
Knowledge Check
At what height h above the earth's surface, the value of g becomes g/2 (where R is the radius of the earth)
A(√2−1)RB√2RC(√2+1)RDR√2The value of gravitational acceleration 'g' at a height 'h' above the earth's surface is g4, then (R = __________ ) (where R = radius of the earth)
Ah = RBh=R2Ch=R3Dh=R4Two identical satellites A and B are circulating round the earth at the height of R and 2 R respectively, (where R is radius of the earth). The ratio of kinetic energy of A to that of B is
A12B23C2D32
A geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. The time period of another satellite at a height of 2.5 R from the surface of the earth is …… hours.
View SolutionThe graph that represents variation of g with depth (d) from the surface of the earth is
View SolutionGiven gd=g(1−dR) where gd and g are the accelerations due to gravity at a depth 'd' km, and on the surface of the Earth, respectively, R is the radius of the Earth, then the depth at which gd=g2 is______.
View SolutionThe graph that represents variation of g with height (h) from the surface of the earth is
View SolutionA geostationary satellite is orbiting the earth at a height of 6R above the surface of the earth, where R is the radius of the earth. What is the time period of another satellite orbiting at a height of 2.5 R from the surface of the earth ?
View Solution

