At the centre of the earth , the value of g becomes
zero
unity
infinity
none of these
The correct Answer is:A
To determine the value of gravitational acceleration (g) at the center of the Earth, we can follow these steps:
1. Understanding the Formula for g:
The acceleration due to gravity (g) at the surface of the Earth is given by the formula:
g=GMR2
where G is the universal gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
Hint: Remember that this formula applies at the surface of the Earth, where the entire mass of the Earth is exerting gravitational force.
2. Considering the Earth as a Uniform Sphere:
For the purpose of this calculation, we assume the Earth is a perfect sphere with uniform density (ρ). The mass of the Earth can be expressed in terms of its density and volume:
M=ρV
where V is the volume of the Earth given by:
V=43πR3
Hint: The volume of a sphere is crucial for relating mass and density.
3. Substituting Volume into the Equation for g:
We can substitute the expression for volume into the equation for mass:
M=ρ(43πR3)
Now substituting this back into the formula for g:
g=G(ρ43πR3)R2
Hint: Simplifying the equation will help us understand how g changes with radius.
4. Simplifying the Expression:
Simplifying the equation gives:
g=43GρR
This shows that g depends on the density of the Earth and the radius.
Hint: Notice that this expression still contains R, which we will evaluate for the center of the Earth.
5. Evaluating g at the Center of the Earth:
At the center of the Earth, the radius R becomes 0. Substituting R=0 into the equation:
g=43Gρ⋅0=0
Hint: Think about why the gravitational force would be zero at the center.
6. Conclusion:
Therefore, the value of gravitational acceleration (g) at the center of the Earth is:
g=0
Final Answer: The acceleration due to gravity at the center of the Earth is zero.
The acceleration due to gravity (g) at the surface of the Earth is given by the formula:
g=GMR2
where G is the universal gravitational constant, M is the mass of the Earth, and R is the radius of the Earth.
For the purpose of this calculation, we assume the Earth is a perfect sphere with uniform density (ρ). The mass of the Earth can be expressed in terms of its density and volume:
M=ρV
where V is the volume of the Earth given by:
V=43πR3
We can substitute the expression for volume into the equation for mass:
M=ρ(43πR3)
Now substituting this back into the formula for g:
g=G(ρ43πR3)R2
Simplifying the equation gives:
g=43GρR
This shows that g depends on the density of the Earth and the radius.
At the center of the Earth, the radius R becomes 0. Substituting R=0 into the equation:
g=43Gρ⋅0=0
Therefore, the value of gravitational acceleration (g) at the center of the Earth is:
g=0
Topper's Solved these Questions
- GRAVITATION BOOK - MCGROW HILL PUBLICATIONCHAPTER - GRAVITATION EXERCISE - HIGHER ORDER THINKING QUESTIONS
25 Videos
- ELECTRIC CURRENT BOOK - MCGROW HILL PUBLICATIONCHAPTER - ELECTRIC CURRENT EXERCISE - HIGHER ORDER THINKING QUESTIONS
29 Videos
- HEATBOOK - MCGROW HILL PUBLICATIONCHAPTER - HEATEXERCISE - HIGHER ORDER THINKING QUESTIONS
15 Videos
Similar Questions
Knowledge Check
At what distance from the centre of the earth, the value of acceleration due to gravity g will be half that on the surface ( R = radius of earth)
A2RBRC1.414RD0.414RAt what height h above the earth's surface, the value of g becomes g/2 (where R is the radius of the earth)
A(√2−1)RB√2RC(√2+1)RDR√2If radius of earth is R, then the height h at which the value of g becomes (1/49)th of its value at the surface is
A2RB3RC6RD4R
At what height from the surface of earth will the value of g becomes 40% from the value at the surface of earth. Take radius of the earth =6.4×106m.
View SolutionThe Earth is not a perfect sphere. Due to the flattening of Earth at the poles, the radius of Earth is minimum at the poles and hence the value of g is maximum at the poles. One the other hand, the radius of the Earth is maximum at the equator of the Earth. As the mass and radius of moon are smaller than that of the Earth, so the value of g on moon is 1.63m/s2 . As we go up from the surface of the Earth, the distance from the centre of the Earth increases and hence the value of g decreases. The value of g decreases as we go down inside the Earth and it become zero at the centre of the Earth .
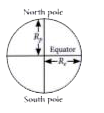
What will be the unit of Gg ?
View SolutionThe Earth is not a perfect sphere. Due to the flattening of Earth at the poles, the radius of Earth is minimum at the poles and hence the value of g is maximum at the poles. One the other hand, the radius of the Earth is maximum at the equator of the Earth. As the mass and radius of moon are smaller than that of the Earth, so the value of g on moon is 1.63m/s2 . As we go up from the surface of the Earth, the distance from the centre of the Earth increases and hence the value of g decreases. The value of g decreases as we go down inside the Earth and it become zero at the centre of the Earth .
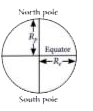
What is the value of acceleration due to gravity on the surface of Earth ?
View SolutionThe Earth is not a perfect sphere. Due to the flattening of Earth at the poles, the radius of Earth is minimum at the poles and hence the value of g is maximum at the poles. One the other hand, the radius of the Earth is maximum at the equator of the Earth. As the mass and radius of moon are smaller than that of the Earth, so the value of g on moon is 1.63m/s2 . As we go up from the surface of the Earth, the distance from the centre of the Earth increases and hence the value of g decreases. The value of g decreases as we go down inside the Earth and it become zero at the centre of the Earth .

If the radius of the Earth were to shrink by 1% and its mass remaining the same, the acceleration due to gravity on the Earth's surface would
View SolutionThe Earth is not a perfect sphere. Due to the flattening of Earth at the poles, the radius of Earth is minimum at the poles and hence the value of g is maximum at the poles. One the other hand, the radius of the Earth is maximum at the equator of the Earth. As the mass and radius of moon are smaller than that of the Earth, so the value of g on moon is 1.63m/s2 . As we go up from the surface of the Earth, the distance from the centre of the Earth increases and hence the value of g decreases. The value of g decreases as we go down inside the Earth and it become zero at the centre of the Earth .
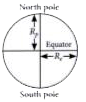
The ratio of acceleration due to gravity ont he Moon and that on the Earth is
View Solution
