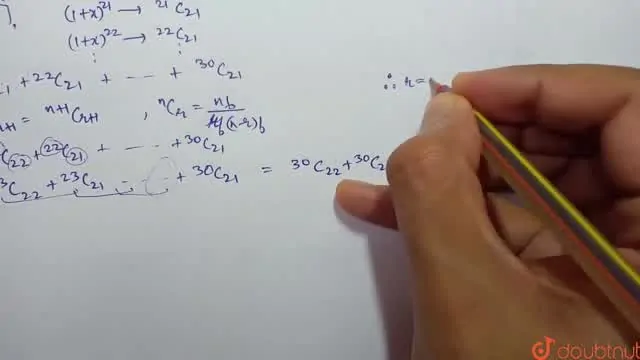If coefficient of x21 in the expansion of (1+x)21+(1+x)22+...+(1+x)30 is 31Cr, where r≥20, then r= ___
The correct Answer is:22
Step by step video, text & image solution for If coefficient of x^(21) in the expansion of (1 + x)^(21) + (1 + x)^(22) + ... + (1 + x)^(30) is ""^(31)C_(r), where r ge 20, then r= ___ by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - EXERCISE (Concept-based Single Correct Answer Type Questions)10videos
MATHEMATICAL INDUCTION AND BINOMIAL THEOREM
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - EXERCISE (LEVEL 1 Single Correct Answer Type Questions)55videos
MATHEMATICAL INDUCTION AND BINOMIAL THEOREM
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - SOLVED EXAMPLES ( LEVEL 2 Single Correct Answer Type Questions)23videos
MATHEMATICAL INDUCTION AND BINOMIAL THEOREM
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - LIMITS AND CONTINUITYEXERCISE - Previous Years B-Architecture Entrance Examination Paper12videos
LIMITS AND CONTINUITY
- BOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL REASONING EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B. ARCHITECTURE ENTRANCE EXAMINATION PAPERS11videos
MATHEMATICAL REASONING
Similar Questions
The coefficient of xr in the expansion of (1−x)−2 is
View Solutionthe coefficient of xr in the expansion of
(1−4x)−1/2, isView SolutionThe coefficient of xr in the expansion of (1−2x)−12 is
View SolutionThe coefficient of x6 in the expansion of (1+x)21+(1+x)22+…+(1+x)30 is
View SolutionThe co-efficient of x5 in the expansion of (1+x)21+(1+x)22+(1+x)23+.....+(1+x)30 is
View SolutionThe coefficient of x10 in the expansion of 1+(1+x)+…+(1+x)20 is
View SolutionThe coefficient of x12 in the expansion of (4x+5x2)21
View SolutionFind the coefficient of x5 in the expansion of (1+x)21+(1+x)22++(1+x)30.
View SolutionFind the coefficient of x5 in the expansion of (1+x)21+(1+x)22++(1+x)30.
View SolutionThe coefficient of x8 in the expansion of 1+(1+x)+(1+x)2+…+(1+x)n(n≥8) is
View Solution