If n is odd, then sum of the series is
0
1
The correct Answer is:A
To solve the problem, we need to evaluate the sum of the series given by:
S=C20−C21+C22−C23+…+(−1)nC2n
where n is an odd integer.
Step 1: Understand the Binomial Coefficient
The binomial coefficient Cnr (or (nr)) represents the number of ways to choose r elements from a set of n elements. The important property we will use is:
Cnr=Cnn−r
Step 2: Write the Series
The series can be rewritten as:
S=n∑r=0(−1)rCnr
Step 3: Use the Binomial Theorem
According to the Binomial Theorem, we have:
(1+x)n=n∑r=0Cnrxr
If we substitute x=−1, we get:
(1−1)n=n∑r=0Cnr(−1)r
Step 4: Evaluate the Left Side
Since n is odd, we have:
0n=0
Thus, we find:
n∑r=0Cnr(−1)r=0
Step 5: Conclusion
This implies that:
S=0
Therefore, the sum of the series is:
0
The binomial coefficient Cnr (or (nr)) represents the number of ways to choose r elements from a set of n elements. The important property we will use is:
The series can be rewritten as:
According to the Binomial Theorem, we have:
Since n is odd, we have:
This implies that:
Topper's Solved these Questions
- MATHEMATICAL INDUCTION AND BINOMIAL THEOREMBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - SOLVED EXAMPLES ( Numerical Answer Type Questions)
20 Videos
- MATHEMATICAL INDUCTION AND BINOMIAL THEOREMBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - EXERCISE (Concept-based Single Correct Answer Type Questions)
10 Videos
- MATHEMATICAL INDUCTION AND BINOMIAL THEOREMBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - SOLVED EXAMPLES ( LEVEL 1 Single Correct Answer Type Questions)
80 Videos
- LIMITS AND CONTINUITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - LIMITS AND CONTINUITYEXERCISE - Previous Years B-Architecture Entrance Examination Paper
12 Videos
- MATHEMATICAL REASONING BOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL REASONING EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B. ARCHITECTURE ENTRANCE EXAMINATION PAPERS
11 Videos
Similar Questions
In C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
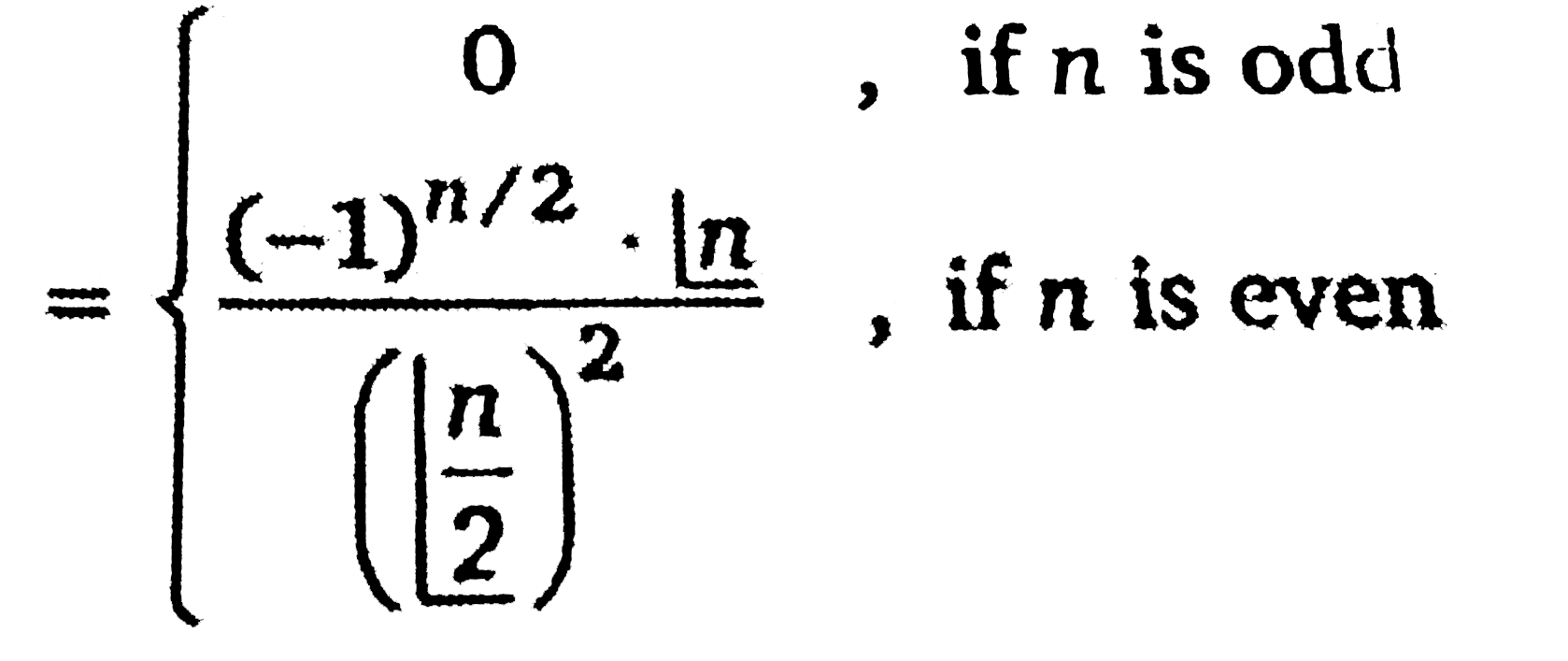
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
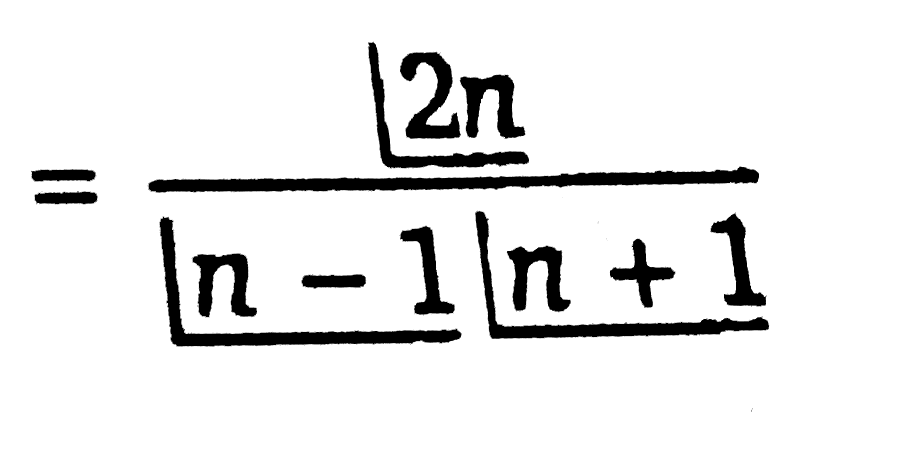
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
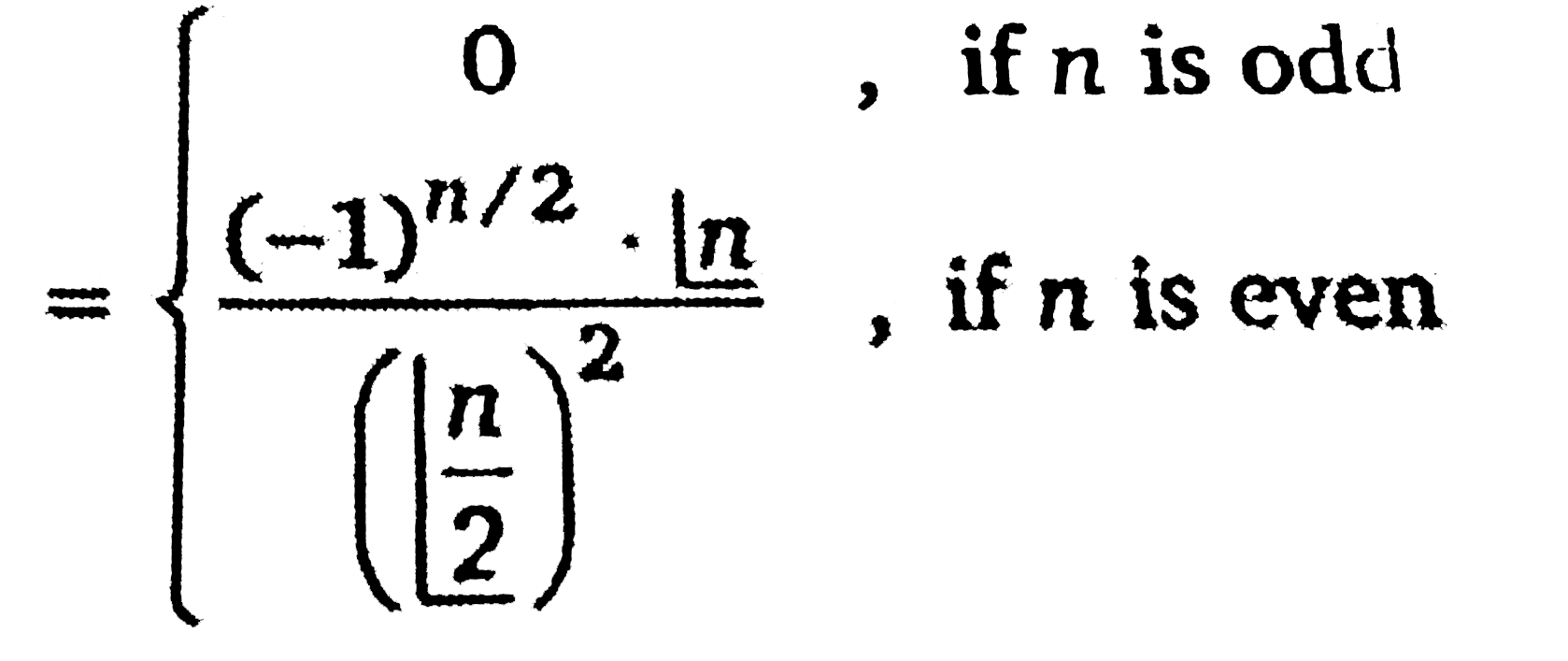
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
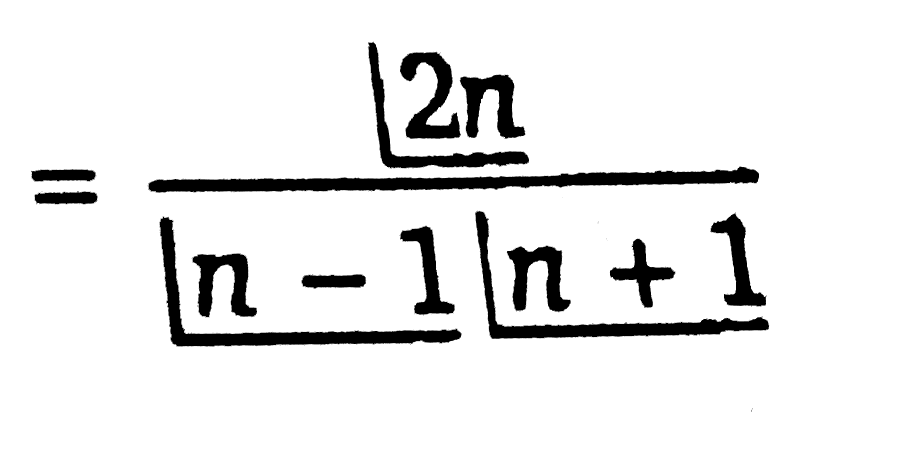
View Solution
Knowledge Check
If C0,C1,C2,…,Cn are coefficients in the
binomial expansion of (1+x)n and n is even , then
C20−C21+C22+C23+...+(−1)nCn2 is equal to .A0B(−1)n/2n![(n2)!]2C(−1)n(2n)!(n!)2D(2n)!(n!)2If Cr stands for nCr then the sum of the series 2(n2)!(n2)!n![C20−2C21+....+(−1)n(n+1)C2n] where n is an even positive integer, is equal to:
A0B(−1)n/2(n+1)C(−1)n/2(n+2)D(−1)nnThe sum of the series n∑r=02nCr, is
A22nB2nC22n+2nCnD12(22n+2nCn)
(C0)2+2(C1)2+3(C2)2+4(C3)2...+(n+1)(cn)2
View SolutionIf (1+x)n=C0+C1x+C2x2+…+Cnxn , prove that
C20−C21+C22−…+(−1)n⋅C2n=0 or
(−1)n/2⋅n!(n/2)!(n/2)!, according as n is odd or even
Also , evaluate C20+C21+C22−...+(−1)n⋅C2n for n
= 10 and n= 11 .
View SolutionProve that C21−2⋅C22+3⋅C23−…−2n⋅C22n=(−1)nn⋅Cn
View SolutionFind the sum C0+3C1+32C2++3nCn.
View SolutionThe sum of the series 3⋅C0+11⋅C1+19⋅C2+27⋅C3+...+(8n+3)⋅Cn is
View Solution
