When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 20 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 25 V, the emf of the battery is
20 V
22 V
15.5 V
14 V
The correct Answer is:B
To find the emf (electromotive force) of the battery, we can analyze the two scenarios provided in the question.
1. Understanding the First Case:
- When a current of 2 A flows from the negative to the positive terminal, the potential difference across the battery is 20 V.
- According to Ohm's law, we can express the relationship as:
V=E−I⋅r
- Here, V is the potential difference (20 V), E is the emf of the battery, I is the current (2 A), and r is the internal resistance of the battery.
- Plugging in the values, we have:
20=E−2r(Equation 1)
2. Understanding the Second Case:
- When a current of 3 A flows in the opposite direction (from positive to negative), the potential difference across the battery is 25 V.
- In this case, the equation becomes:
V=E+I⋅r
- Here, V is now 25 V, I is 3 A, so we write:
25=E+3r(Equation 2)
3. Solving the Equations:
- Now we have two equations:
- From Equation 1: E=20+2r
- From Equation 2: E=25−3r
- We can set these two expressions for E equal to each other:
20+2r=25−3r
- Rearranging gives:
2r+3r=25−20
5r=5
r=1ohm
4. Finding the Emf:
- Now substitute r=1 back into either equation for E. Using Equation 1:
E=20+2(1)=20+2=22V
Final Answer:
The emf of the battery is 22 V.
- When a current of 2 A flows from the negative to the positive terminal, the potential difference across the battery is 20 V.
- According to Ohm's law, we can express the relationship as:
V=E−I⋅r
- Here, V is the potential difference (20 V), E is the emf of the battery, I is the current (2 A), and r is the internal resistance of the battery.
- Plugging in the values, we have:
20=E−2r(Equation 1)
- When a current of 3 A flows in the opposite direction (from positive to negative), the potential difference across the battery is 25 V.
- In this case, the equation becomes:
V=E+I⋅r
- Here, V is now 25 V, I is 3 A, so we write:
25=E+3r(Equation 2)
- Now we have two equations:
- From Equation 1: E=20+2r
- From Equation 2: E=25−3r
- We can set these two expressions for E equal to each other:
20+2r=25−3r
- Rearranging gives:
2r+3r=25−20
5r=5
r=1ohm
- Now substitute r=1 back into either equation for E. Using Equation 1:
E=20+2(1)=20+2=22V
The emf of the battery is 22 V.
Topper's Solved these Questions
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - MCQs AIPMT / NEET
32 Videos
- CURRENT ELECTRICITY BOOK - MTG GUIDECHAPTER - CURRENT ELECTRICITY EXERCISE - NEET CAFE ( TOPICWISE PRACTICE QUESTIONS )
199 Videos
- ATOMS AND NUCLEIBOOK - MTG GUIDECHAPTER - ATOMS AND NUCLEIEXERCISE - AIPMT/NEET(MCQs)
40 Videos
- DUAL NATURE OF MATTER AND RADIATION BOOK - MTG GUIDECHAPTER - DUAL NATURE OF MATTER AND RADIATION EXERCISE - AIPMT/ NEET MCQs
30 Videos
Similar Questions
The potential difference across terminals of a battry is 9.0V, when a current of 3.5A flows through it from its negative terminal to the positive terminal .When a current of 2A flows through in the opposite direction, the terminal potential difference is 12V. Find the internal resistance and emf of the battery
View SolutionThe potential difference across the terminals of a battery is 8.4V when there is a current of 1.50A in the battery from the negative to the positive terminal. When the current is 3.50Air, the reverse direction, the potential difference becomes 9.4V.
(a) What is the internal resistance of the battery?
(b) What is the emf of the battery?
View Solution
Knowledge Check
When a current of 2 A flows in a battery from negative to positive terminal, the potential difference across it is 12 V. If a current of 3 A flowing in the opposite direction produces a potential difference of 15 V, the emf of the battery is
A12.6VB13.2VC13.5VD14.0VPotential difference across the terminal of a non ideal battery is
Azero when it is short circuitedBless than its emf when current flows from negative terminal to positive terinal inside the batteryCzero when no current is drawn from the batteryDgreater than its emf when current flows from positive terminal to negative terminal inside the batteryA current of 2A flows in a system of conductor as shown. The potential difference (VA−VB)
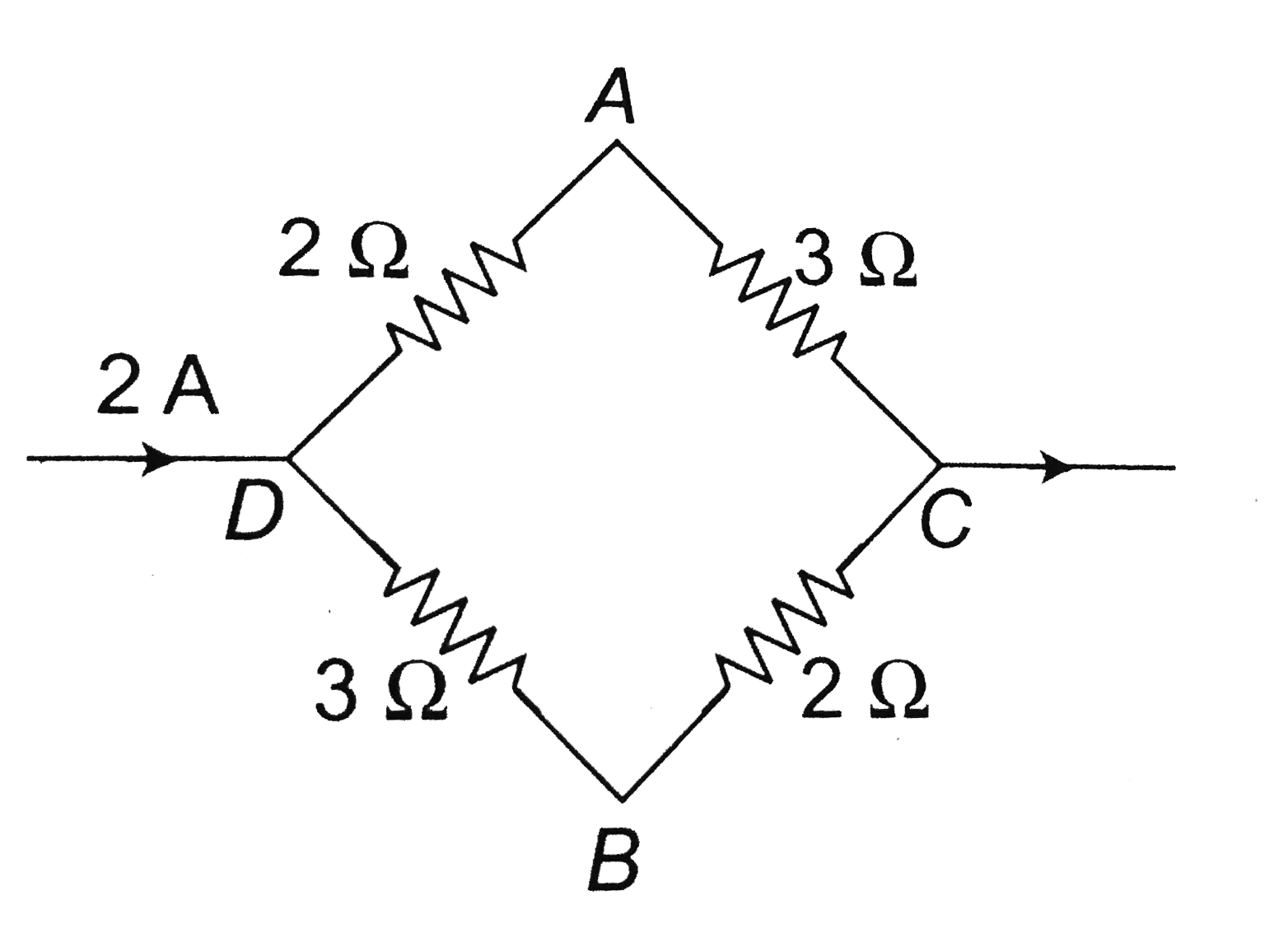 A+2VB+1VC−1VD−2V
A+2VB+1VC−1VD−2V
Can the potential difference across a battery be greater than its emf?
View SolutionWhen a current drawn from a battery is 0.5 A, its terminal potential difference is 20 V. And when current drawn from it is 0.2 A, the terminal voltage reduces to 16 V. Find out, emf and internal resistance of the battery.
View SolutionThe potential difference across te terminals of a battery is 10 V when there is a current of 3 A in the battery from the negative to the positive terminal. When the current is 2A in the reverse direction, the potential difference becomes 15 V. The internal resistance of the battery is
View SolutionIf the potential difference across the ends of a conductor is doubled, the current flowing through it gets
View SolutionIf a power of 100 W is being supplied across a potential difference of 200 V , current flowing is
View Solution
