Under the action of a given coulombic force the acceleration of an electron is 3.5×1025ms−2. Then the magnitude of the acceleration of a proton under the action of same force is nearly
1.6×10−19ms−2
9.1×1031ms−2
1.9×1022ms−2
1.6×1027ms−2
The correct Answer is:C
To solve the problem, we need to find the acceleration of a proton when the same Coulombic force is applied to it as that which is applied to an electron. We will use Newton's second law of motion, which states that force (F) is equal to mass (m) times acceleration (a), or F=ma.
1. Identify the given values:
- Acceleration of the electron (ae) = 3.5×1025m/s2
- Mass of the electron (me) = 9.1×10−31kg
- Mass of the proton (mp) = 1.7×10−27kg
2. Apply Newton's second law:
- For the electron, the force can be expressed as:
F=me⋅ae
- For the proton, the force is:
F=mp⋅ap
- Since the force is the same for both the electron and the proton, we can set the two equations equal:
me⋅ae=mp⋅ap
3. Rearranging the equation:
- We can rearrange the equation to find the acceleration of the proton (ap):
ap=memp⋅ae
4. Substituting the values:
- Substitute the known values into the equation:
ap=9.1×10−311.7×10−27⋅(3.5×1025)
5. Calculating the mass ratio:
- Calculate the mass ratio:
9.1×10−311.7×10−27≈5.35×10−4
6. Calculating the acceleration of the proton:
- Now, substitute this ratio back into the equation for ap:
ap≈(5.35×10−4)⋅(3.5×1025)≈1.87×1022m/s2
7. Final approximation:
- We can approximate 1.87×1022 to 1.9×1022m/s2.
Final Answer:
The magnitude of the acceleration of the proton under the action of the same force is approximately 1.9×1022m/s2.
---
- Acceleration of the electron (ae) = 3.5×1025m/s2
- Mass of the electron (me) = 9.1×10−31kg
- Mass of the proton (mp) = 1.7×10−27kg
- For the electron, the force can be expressed as:
F=me⋅ae
- For the proton, the force is:
F=mp⋅ap
- Since the force is the same for both the electron and the proton, we can set the two equations equal:
me⋅ae=mp⋅ap
- We can rearrange the equation to find the acceleration of the proton (ap):
ap=memp⋅ae
- Substitute the known values into the equation:
ap=9.1×10−311.7×10−27⋅(3.5×1025)
- Calculate the mass ratio:
9.1×10−311.7×10−27≈5.35×10−4
- Now, substitute this ratio back into the equation for ap:
ap≈(5.35×10−4)⋅(3.5×1025)≈1.87×1022m/s2
- We can approximate 1.87×1022 to 1.9×1022m/s2.
The magnitude of the acceleration of the proton under the action of the same force is approximately 1.9×1022m/s2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - AIPMT/NEET (MCQ.s)
34 Videos
- ELECTROSTATICSBOOK - MTG GUIDECHAPTER - ELECTROSTATICSEXERCISE - NEET ITALS
1 Videos
- ELECTRONIC DEVICESBOOK - MTG GUIDECHAPTER - ELECTRONIC DEVICESEXERCISE - AIPMT/NEET (MCQs)
42 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBOOK - MTG GUIDECHAPTER - MAGNETIC EFFECTS OF CURRENT AND MAGNETISMEXERCISE - AIPMT/NEET (MCQs)
48 Videos
Similar Questions
Knowledge Check
Under the action of a given coulombic force the acceleration of an electron is 2.5×1022ms−1. Then, the magnitude of the acceleration of a proton under the action of same force is nearly
A1.6×10−19ms−2B9.1×1031ms−2C1.5×1019ms−2D1.6×1027ms−2Calculate the coulomb force between two electrons separated by 0.8×10−15m.
A300NB360NC340ND320NElectric charges under action of electric forces is called
AelectrostaticBelectric fluxCelectric fieldDelectric field lines
A body under the action of several forces will have zero acceleration
View SolutionUnder the action of variable force, at any instant the displacement is
View SolutionA body is inequibrium under the action of three coplanar forces, then
View SolutionUnder the action of force P, the constant acceleration of block B is 3ms−2 to the right. At the instant when the velocity of B is 2ms−1 to the right, determine the velocity of B relative to A, the acceleration of B relative to A and the absolute velocity of point C of the cable.

View SolutionUnder the action of force P, the constant acceleration of block B is 6m/sec2 up the incline. For the instant when the velocity of B is 3m/sec up the incline. Choose the correct option(s)
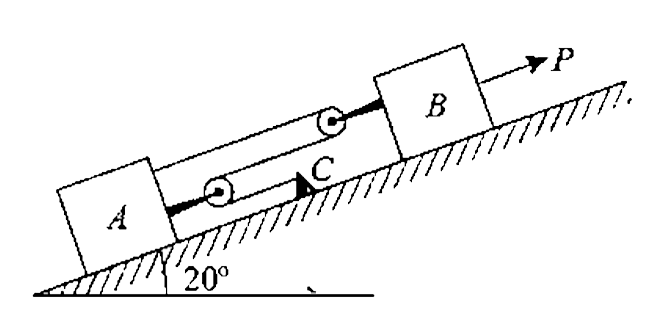
View Solution
