Find the area of the region bounded by the two parabolas $y = x^{2}$ and $y^{2} = x$ .

Video Solution

Text Solution

Verified by Experts

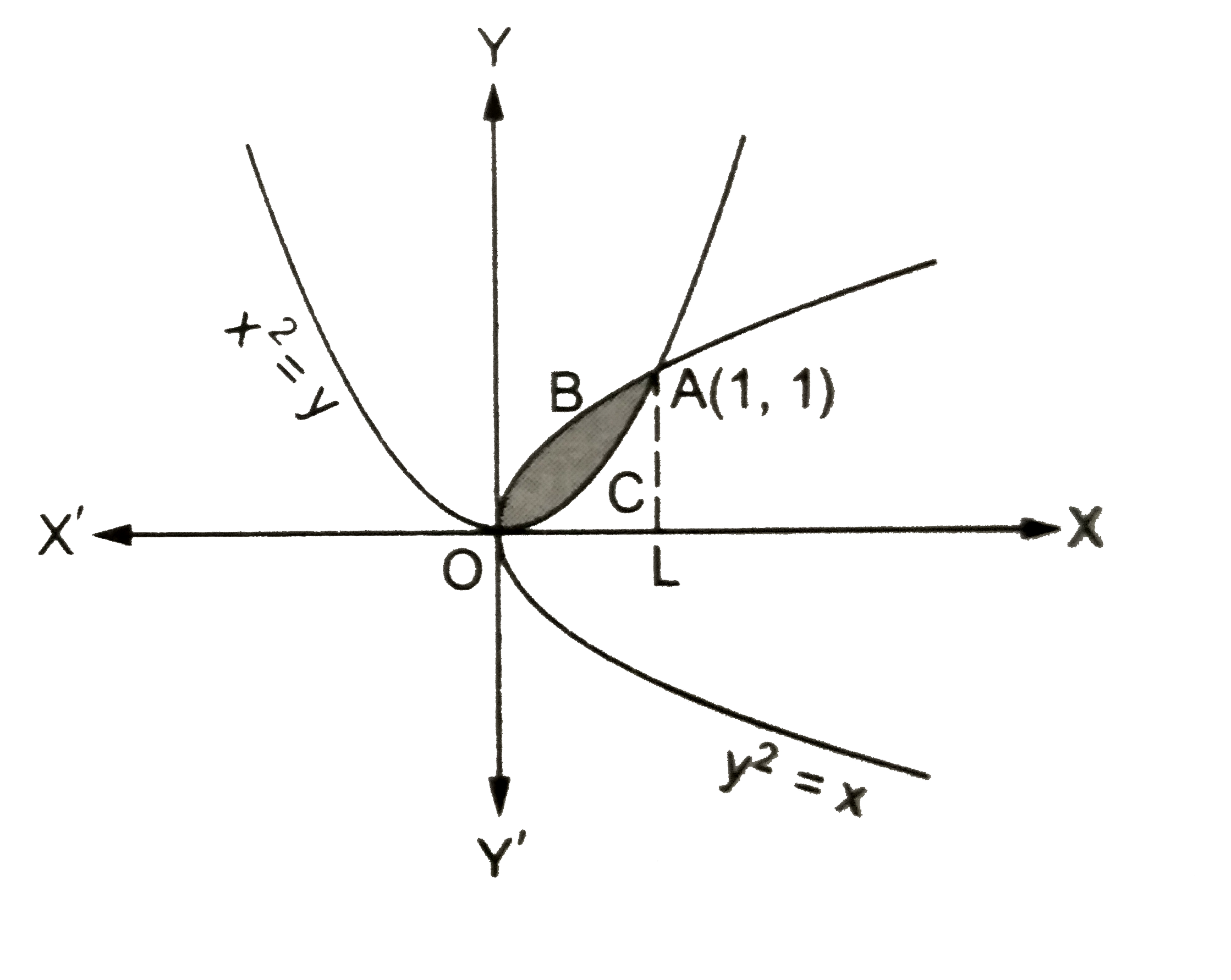
Clearly $x^{2} = y$ is an upward parabola with is vertex at (0,0) and $y^{2} = x$ is right -handed parabola with its vertex also at (0,0).The shaded region shows the area bounded by these parabolas.

The given equations are
$x^{2} = y$
and $y^{2} = x$
Using (i) in (ii) we get
$x^{4} = x \Rightarrow (x^{3} - 1) = 0 \Rightarrow x = 0 or x = 1$
Also $(x = 0 \Rightarrow y = 0) and (X = 1 \Rightarrow y = 1)$
So , the given curves intersect at O (0,0) and A(1,1)
Draw $A L ⊥ O X$
Required area =(area OLABO)-(area OLACO)
= (area bounded by $x^{2} = y$ from x =0 to x=1}
$= 1 \int 0 \sqrt{x} dx - 1 \int 0 x^{2} d x$
$= {[\frac{2}{3} x^{3 / 2}]}_{0}^{3 / 2} - {[\frac{x^{3}}{3}]}_{0}^{1} = (\frac{2}{3} - \frac{1}{3}) = \frac{1}{3}$ sq unit.
Hence , the required area is $\frac{1}{3}$ sq unit

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

What is the area of the region bounded by the parabola $y^{2} = 6 (x - 1)$ and $y^{2} = 3 x$ ?
AA. $\frac{\sqrt{6}}{3}$
BB. $\frac{2 \sqrt{6}}{3}$
CC. $\frac{4 \sqrt{6}}{3}$
DD. $\frac{5 \sqrt{6}}{3}$

RS AGGARWAL-AREA OF BOUNDED REGIONS -Exercise 17

Home
Ask Doubt
Profile