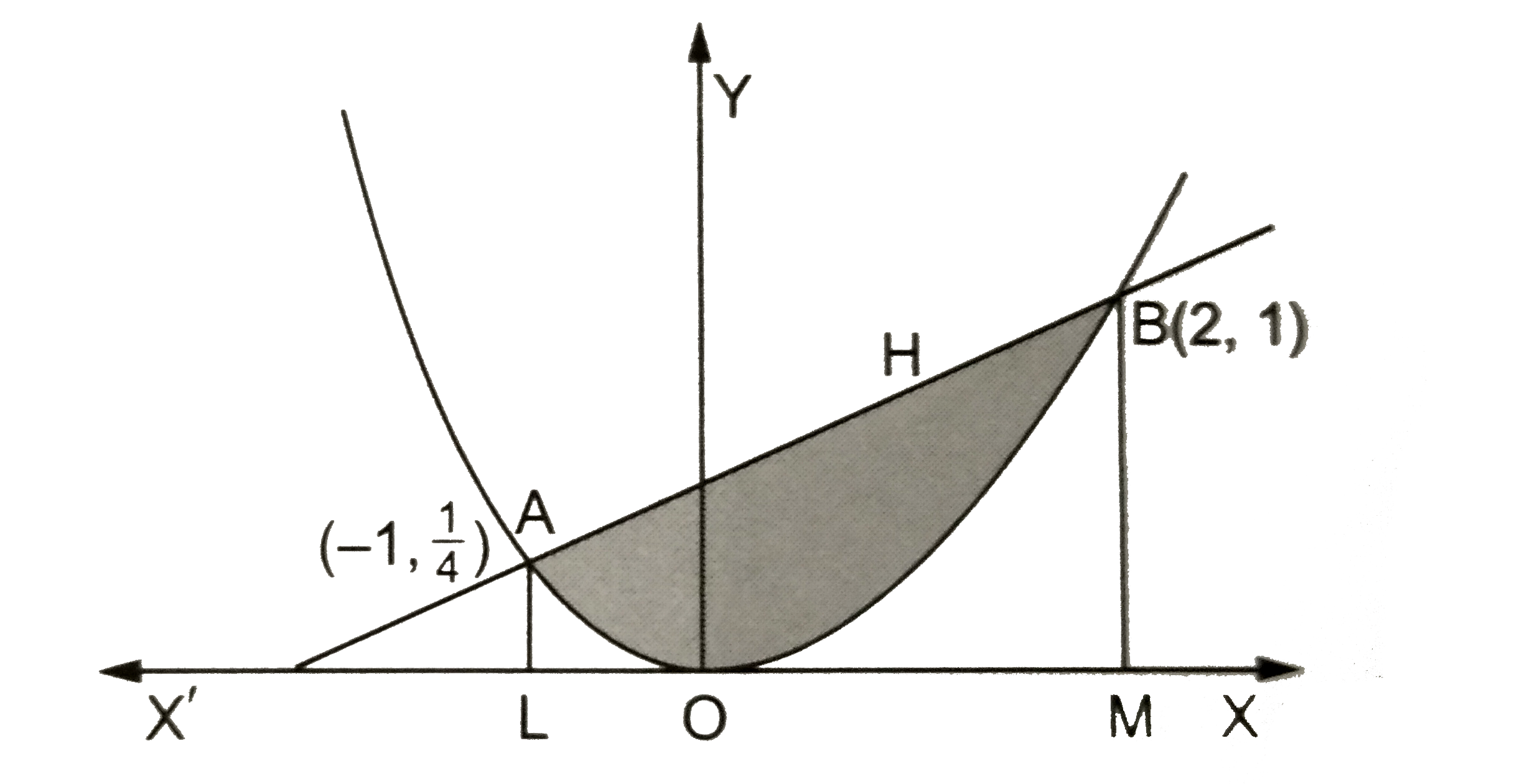
Find the area of the region bounded by the parabola x2=4y\ and the line x=4y−2
The given curve is x2=4y
The given line is x=4y -2
Putting 4y= (x+2) from (ii) into (i) we get
x2=(x+2)⇔(x2−x−2)=0
⇔(x−2)(x+1)=0
⇔x=2orx=−1
Putting x =2 in (i) we get y=-1
Putting x =-1 in (i) weget y=14
Thus the points of intersection of the given curve (i) and the line (ii) are A(−1,14) and B (2,1)
Draw AL and BM are perpendiculars on the x-axis
∴ required are= area AOBA
=(area ALMBA )- (area AOMLA)
2∫−1(x−24)dx−2∫−1x24dx
=2∫−1{(x+24)−x24}dx=14[x22+2x=x33]2−1
14[(2+4−83)−(12−2+13)]=98sq units
Related Playlists
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions89videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 3018videos
BAYES'S THEOREM AND ITS APPLICATIONS
Similar Questions
Find the area of the region bounded by the parabola x2=4y\ and the line x=4y−2
View SolutionUsing integration, find the area of the region bounded by the parabola y2=4x and the line x=4.
View SolutionUsing integration, find the area of the region bounded by the parabola y2=16x and the line x=4
View SolutionFind the area of the regions bounded by the parabola y2=4ax and the line x=a.
View SolutionFind the area of the region bounded by the parabola y2=4ax and the line x=a.
View SolutionFind the area of the region bounded by the parabola y2=25x and the line x =5
View SolutionFind the area of the region bounded by the parabola y2=2x and the line x−y=4
View SolutionFind the area of the region bounded by the parabola y2=16x and the line x=4.
View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View SolutionFind the area of the region bounded by the parabola y2=8x and the line x=2
View Solution


