For a reactionK(1+10)K(1)=x. When temperature is increased from 10∘C to 100∘C rate constnat (K) increased by a factor of 512. Then value of x is Solution in Telugu
1.5
2.5
3
2
The correct Answer is:D
Step by step video, text & image solution for For a reaction(K_((1+10)))/(K_((1)))=x. When temperature is increased from 10^(@)C to 100^(@)C rate constnat (K) increased by a factor of 512. Then value of x is by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETICSBook:AAKASH SERIESChapter:CHEMICAL KINETICSExercise:OBJECTIVE EXERCISE - 1 (Collision theory)
Explore 14 Videos
- CHEMICAL KINETICSBook:AAKASH SERIESChapter:CHEMICAL KINETICSExercise:OBJECTIVE EXERCISE - 1 (Order, molecularity and half life)
Explore 43 Videos
- CHEMICAL KINETICSBook:AAKASH SERIESChapter:CHEMICAL KINETICSExercise:Subjective Exercise -4 (Numerical Problems)
Explore 7 Videos
- CHEMICAL KINETCSBook:AAKASH SERIESChapter:CHEMICAL KINETCSExercise:EXERCISE - 3.2
Explore 45 Videos
- CHEMICAL THERMODYNAMICSBook:AAKASH SERIESChapter:CHEMICAL THERMODYNAMICSExercise:Additional Practice Exercise
Explore 54 Videos
Similar Questions
For a reversible reaction, A⇔B, which one of the following statements is wrong from given energy profile diagram ?
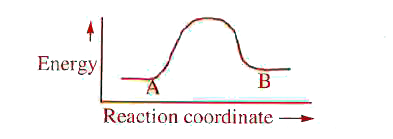
View SolutionWhich of the following is correct ?
View SolutionThe initial concentration of [A] = 0.3 mol/lit. The concentration after 2.3 min is 0.15 moles/lit. What is the value of rate constant.
View SolutionDiscuss on the kinetic spontaneity of a chemical reaction. Is a slow reaction spontaneous? Why?
View SolutionWhich among the following is not an exact differential?
View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10∘C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10∘C change in temperature.
Temperature coefficient(μ)=Rate constant of(T+10)∘CRate constant atT∘C
Arrhenius gave an equation which describes aret constant k as a function of temperature
k=Ae−Ea/RT
where k is the rate constant, A is the frequency factor or pre-exponential factor, Ea is the activation energy, T is the temperature in kelvin, R is the universal gas constant.
Equation when expressed in logarithmic form becomes
logk=logA−Ea2.303RT
For the given reactions, following data is given
P→Qk1=1015exp(−2000T)C→Dk2=1014exp(−1000T)
Temperature at which k1=k2 is
View SolutionBy increasing the temperature by 10∘C, the rate of forward reaction at equilibrium is increased by a factor of 2. The rate of backward reaction by this increase in temperature
View SolutionThe rate of reaction is doubled for 10∘C rise in temperature. The increase in the reaction rate as a result of temperature rise from 10∘C to 100∘C is
View SolutionThe rate of a reaction is doubled for every 10^(@)C rise in temperature . The increase in reaction rate as a result of temperature rise from 10^(@) C to 100^(@)C is
View SolutionIn a zero order reaction for every 10∘C rise of temperature , the rate is double . If the temperature is increased from 10∘C to 100∘C , the rate of the reaction will become -
View SolutionFor a reaction (K_((1+10)))/(K_((1)))=x . When temperature is increased from 10^(@)C to 100^(@)C rate constnat (K) increased by a factor of 512. Then value of x is
View SolutionThe rate of a reaction is doubled for every 10^@C rise in temperature. The increase in rate as a result of increase in temperature from 10^@C to 100^@C is:
View SolutionThe rate of a reaction is doubled for every 10^@C rise in temperature. The increase in rate as a result of increase in temperature from 10^@C to 100^@C is:
View SolutionThe rate of reaction increases isgnificantly with increase in temperature. Generally, rate of reactions are doubled for every 10∘C rise in temperature. Temperature coefficient gives us an idea about the change in the rate of a reaction for every 10∘C change in temperature.
Temperature coefficient(μ)=Rate constant of(T+10)∘CRate constant atT∘C
Arrhenius gave an equation which describes aret constant k as a function of temperature
k=Ae−Ea/RT
where k is the rate constant, A is the frequency factor or pre-exponential factor, Ea is the activation energy, T is the temperature in kelvin, R is the universal gas constant.
Equation when expressed in logarithmic form becomes
logk=logA−Ea2.303RT
For the given reactions, following data is given
P→Qk1=1015exp(−2000T)C→Dk2=1014exp(−1000T)
Temperature at which k1=k2 is
View SolutionIn a zero-order reaction for every 10∘ rise of temperature, the rate is doubled. If the temperature is increased from 10∘C to 100∘C, the rate of the reaction will become
View Solution

