A certain endothermic reaction: A→ Product, ΔH=+ve proceeds ina sequence of three elementary steps with the rate constant K1,K2 and K3 and each one having energy of activation E1,E2 and E3 respectively at 25∘C. The observed rate constannt for the reaction is equal to K3√K1K2.
A1,A2 and A3 are Arrhenius parameters respectively.
If temperature coefficient of the observed reactionis 2,the numerical value of E1−E2+2E3 is Solution in Telugu
12.73 kcal
25.4 kcal
38.19 kcal
cannot be calculated
The correct Answer is:B
log(K2K1)=Ea2.303R(1T1−1T2),log(2)=εa2.3.3R(1298−1308)
εa=(0.3010×2.303×2×298×30810),εa=12.72KCal=(2ε3+ε1−ε22)
12.72=(2ε3+ε1−ε22)(2ε3+ε1−ε2)=12.72×2=25.4499,(ε1−ε2+2ε3)≅25.4 Kcal
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-III MATCH THE FOLLOWING QUESTIONS)3videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-IV INTEGER ANSWER TYPE QUESTIONS)10videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETICSEXERCISE - LEVEL-II(LECTURE SHEET EXERCISE-I SINGLE & ONE OR MORE THAN ONE CORRECT ANSWER)50videos
CHEMICAL KINETICS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL KINETCSEXERCISE - EXERCISE - 3.245videos
CHEMICAL KINETCS
- BOOK - AAKASH SERIESCHAPTER - CHEMICAL THERMODYNAMICSEXERCISE - Additional Practice Exercise54videos
CHEMICAL THERMODYNAMICS
Similar Questions
Match the following columns
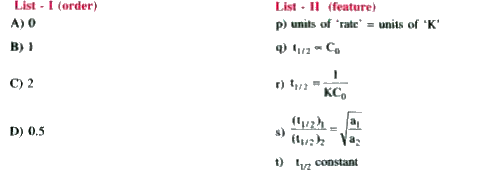 03:57View Solution
03:57View SolutionFor the reaction A→ products the following dats is given for a particular run
time (in): 0 5 15 35
1[A](M−1):1 2 4 8
Determine the order of the reaction.04:14View SolutionThe rate constant of a a reaction depends on
04:14View SolutionDiscuss on the kinetic spontaneity of a chemical reaction. Is a slow reaction spontaneous? Why?
04:46View SolutionWhich among the following is not an exact differential?
03:26View SolutionA reaction takes place in theee steps: the rate constant are k_(1), k_(2), and k_(3) . The overall rate constant k=(k_(1)k_(3))/(k_(2)) . If E_(1), E_(2) , and E_(3) (energy of activation) are 60, 30 and 10kJ , respectively, the overall energy of activation is
04:32View SolutionA certain endothermic reaction: Ararr Product, DeltaH=+ve proceeds in a sequence of three elementary steps with the rate constants K_(1), K_(2) and K_(3) and each one having energy of activation E_(a), E_(2) and E_(3) respectively at 25^(@)C . The observed rate constant for the reaction is equal to K_(3) sqrt(K_(1)/K_(2)). A_(1), A_(2) and A_(3) are Arrhenius parameters respectively. The observed energy of activation for the reaction is:
View SolutionA certain endothermic reaction: Ararr Product, DeltaH=+ve proceeds in a sequence of three elementary steps with the rate constants K_(1), K_(2) and K_(3) and each one having energy of activation E_(a), E_(2) and E_(3) respectively at 25^(@)C . The observed rate constant for the reaction is equal to K_(3) sqrt(K_(1)/K_(2)). A_(1), A_(2) and A_(3) are Arrhenius parameters respectively. The observed Arrhenius parameter for the reaction is:
03:46View SolutionA certain endothermic reaction: Ararr Product, DeltaH=+ve proceeds in a sequence of three elementary steps with the rate constants K_(1), K_(2) and K_(3) and each one having energy of activation E_(a), E_(2) and E_(3) respectively at 25^(@)C . The observed rate constant for the reaction is equal to K_(3) sqrt(K_(1)/K_(2)). A_(1), A_(2) and A_(3) are Arrhenius parameters respectively. Presence of a catalyst decreases the energy of activation of each path by half the value of E_(1) . Assuming the order actors same, the observed energy of activation would be:
01:28View SolutionA certain endothermic reaction: A→ Product, ΔH=+ve proceeds in a sequence of three elementary steps with the rate constants K1,K2 and K3 and each one having energy of activation Ea,E2 and E3 respectively at 25∘C. The observed rate constant for the reaction is equal to K3√K1K2.A1,A2 and A3 are Arrhenius parameters respectively.
Which represents the correct value, if catalyst is not present?02:41View SolutionA certain endothermic reaction: A→ Product, ΔH=+ve proceeds in a sequence of three elementary steps with the rate constants K1,K2 and K3 and each one having energy of activation Ea,E2 and E3 respectively at 25∘C. The observed rate constant for the reaction is equal to K3√K1K2.A1,A2 and A3 are Arrhenius parameters respectively.
If temperature coefficient of the observed reaction is 2, the numerical value of E1−E2+2E3 is:02:52View SolutionA certain endothermic reaction: Ararr Product, DeltaH=+ve proceeds in a sequence of three elementary steps with the rate constants K_(1), K_(2) and K_(3) and each one having energy of activation E_(a), E_(2) and E_(3) respectively at 25^(@)C . The observed rate constant for the reaction is equal to K_(3) sqrt(K_(1)/K_(2)). A_(1), A_(2) and A_(3) are Arrhenius parameters respectively. For the reaction, H^(.)+^(.)CH_(2)CH_(3)overset(K)(rarr) CH_(3).CH_(3) , a chain termination step of the reaction: 2C_(2)H_(6)rarr CH_(2)=CH_(2)+H_(2) , the activation energy and Arrhenius parameter can be given as:
View SolutionA certain endothermic reaction: Ararr Product, DeltaH=+ve proceeds in a sequence of three elementary steps with the rate constants K_(1), K_(2) and K_(3) and each one having energy of activation E_(a), E_(2) and E_(3) respectively at 25^(@)C . The observed rate constant for the reaction is equal to K_(3) sqrt(K_(1)/K_(2)). A_(1), A_(2) and A_(3) are Arrhenius parameters respectively. For a reversible reaction, A underset(K_(2))overset(K_(1))(hArr) B, DeltaH=q , if perexponential factors are same. The correct relation is:
06:14View SolutionA reaction takes place in three steps. The rate constant are k1,k2 and k3. The overall rate constant k=k1k3k2. If E1,E2 and E3 (energy of activation) are 60, 30 and 10 kJ, respectively, the overall energy. Of activation is
04:21View SolutionA reaction takes place in three steps with individual rate constant and activation energy,
Rate constantActivation energyStep 1k1Ea1=180kJ/molStep2k2Ea2=180kJ/molStep3k3Ea3=180kJ/mol
oveall rate constant, k=(k1k2k3)2/3 overall activation energy of the reaction will be :05:42View SolutionA reactant (A) forms two products : A overset(k_(1))to B , Activation Energy E_(a_(1)) A overset(k_(2))to C , Activation Energy E_(a_(2)) If E_(a_(2))=2E_(a_(1)) , then k_(1) and k_(2) are related as
03:15View Solution
