मान ले कि दो पारदर्शी माध्यमों के बीच सीमा x-y तल से दी जाती है | $z \geq 0$ में माध्यम 1 का अपवर्तनांक $\sqrt{2}$ है और $z < 0$ में माध्यम 2 का अपवर्तनांक $\sqrt{3}$ है | सदिश $\to A = 5 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j = 10 ˆ k$ से दी गई माध्यम 1 में प्रकाश की किरण पृथक्कारी तल पर आपतित है | माध्यम 2 में अपवर्तन कोण है

A

$30^{\circ}$

B

$45^{\circ}$

C

$60^{\circ}$

D

$75^{\circ}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

इकाई सदिश तल को लंबवत दर्शाता है |
${ˆ e}_{n} = ˆ k$ .
आपतित किरण का लम्ब के परितः भाग है
$- 1 ˆ k$ .
इकाई सदिश जो कि आपतित किरण को समतल तथा लंबवत दर्शाता है
${ˆ e}_{p} = \frac{6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j}{\sqrt{{(6 \sqrt{3})}^{2} + {(8 \sqrt{3})}^{2}}} = 0.6 ˆ i + 0.8 ˆ j$
आपतित किरण और लम्ब के बीच का कोण होगा
$cos θ = (6 \sqrt{3} ˆ i + 8 \sqrt{3} ˆ j - 10 ˆ k)$
$. ˆ k / {(6 \sqrt{3})}^{2} + {(8 \sqrt{3})}^{2} + 10^{2}$
or $cos θ = - 0.5$
अतः कोण $θ = 120^{\circ}$

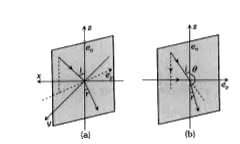
आपतित कोण है $i = 180^{\circ} - 120^{\circ} = 60^{\circ}$
किरण का परावर्तन कोण
$\sqrt{2} sin (i) = \sqrt{3} sin (r) or r = 45^{\circ}$
अतः आवश्यक किरण का समीकरण है $cos (r) {ˆ e}_{n} + sin (r) {ˆ e}_{p}$
$= cos (45^{\circ}) (- ˆ k) + sin (45^{\circ}) \cdot (0.6 ˆ i + 0.8 ˆ j)$
$= \frac{1}{\sqrt{2}} (0.6 ˆ i + 0.8 ˆ j - ˆ k)$

Updated on:21/07/2023

|

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

ERRORLESS HINDI-किरण प्रकाशिकी-Ordinary Thinking Objective Questions (समतल सतह पर प्रकाश का अपवर्तन)

Home
Ask Doubt
Profile