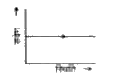
हर प्रकार की गतिकीय समस्याओं के विश्लेषण के लिए फेज समष्टि चित्रम ( Phase space diagrams ) का उपयोग किया जाता है। प्रारंभिक दशा, स्थिति व् सवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझाने में बहुत उपयोगी है। यहाँ हम एक विमीय सरल गतिकीय निकायों की बात करते है । इनके संवेग Y - अक्ष पर रखते है। तब फेज समष्टि चित्राम इस समतल में एक x(t)vs.p(t) (i ) वक्र होता। वक्र पर तीर समय बढ़ाने की दिशा दर्शाता है। उदाहरण के लिए, स्थिर वेग से चल रहें कण के लिए फेज समष्टि चित्राम सरल रेखा है जिसे चित्र में दिखाया गया है। चिन्ह परिपाटी में स्थित या संवेग को ऊपर (या दाहिने ) और धनात्मक तथा निचे (या बायीं) और ऋणात्मक मान जाता है
सरल आवर्त दोलन (SHM ) का फेज समष्टि चित्राम उदगम पर केंद्रित वृत है। चित्र में दर्शया गए दो वृत, एक ही दोलक के लिए है, जब उसकी आरंभिक अवस्थाएं भिन्न है ,तथा E1 व् E2 क्रमशः दोलक की कुल यांत्रिक ऊर्जाएं है। तब
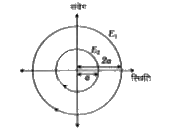
E1=√2E2
E1=2E2
E1=4E2
E1=16E2
The correct Answer is:C
प्रथम स्थिति में SHM का आयाम a है
प्रथम स्थिति में SHM का आयाम 2a है।
कुल ऊर्जा =12 (आयाम )2
E1=12k(2a)2.E2=12(a)2
E1=4E2
वैकल्पिक ,
रेखिक संवेग P = mv
=mω√A2−X2
⇒P2=m2ω2(A2−x2)
⇒P2+(mω)2x2=m2ω2A2
वृत का समीकरण (बड़ा)
P2+x2=(2a)2
P2+x2=4a2
वृत का समीकरण (छोटा)
P2+x2=a2
(i) व् (ii ) तुलना करने पर आयाम A = 2a
तथा (mω)2=1⇒mω2=1m
इसलिए ऊर्जा 12mω2(A)2
E1=12mω2(2a)2
=121m×(4a2)=2a2m
(i ) व् (iii ) की तुलना करने पर
A=a
(mω)2=1⇒mω2=1m
इसलिए , E2=12mω2A2=12×1ma2=12a2m2
इसलिए ,E1E2=4⇒E1=4E2.
Topper's Solved these Questions
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:JEE Section (Integer type questions)
Explore 1 Video
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:JEE Section (Matrix Match Type Questions)
Explore 3 Videos
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:JEE Section (Reasoning Type Questions)
Explore 2 Videos
- विधुत चुम्बकीय प्रेरण Book:ERRORLESS HINDIChapter:विधुत चुम्बकीय प्रेरण Exercise:Self Evaluation Test विधुत चुम्बकीय प्रेरण
Explore 17 Videos
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Self Evaluation Test
Explore 8 Videos
Similar Questions
0.8 किग्रा द्रव्यमान का एक कण 1.0 मीटर के आयाम और आवर्त समय 117 सेकण्ड के साथ सरल आवर्त गति कर रहा है। उस समय कण की गतिज ऊर्जा की गणना करें जब उसका विस्थापन 0.6 मीटर हो।
View Solutionसरल आवर्त गति करने वाले कण का त्वरण-विस्थापन (a-x) ग्राफ चित्र में दिखाया गया है। दोलन की आवृत्ति ज्ञात कीजिए।
View Solutionयदि बल नियतांक क्रमशा k1 एवं k2 वाली दो कमानियां, S1 एवं S2 एक समान बल से तानित की जाए, तब यह पाया जाता है, की कमानी S1 पर कमानी S2 के मुकाबले अधिक कार्य किया जाता है।
कथन-I : यदि कमानियां एकसमान मात्रा से तनित की जाती है , तब S1 पर किया गया कार्य S2 पर किये गए कार्य से अधिक है
कथन-2 : k1<k2
View Solutionचित्र में चार तार लूपो को दिखाया गया है। जिनकी भुजाओ की लम्बाई L या 2L है सभी चारो एकसमान वेग से एक समरूप चुम्बकीय क्षेत्र →B (कागज़ तल के लम्बवत बाहर की ओर) से गुजरते है। जब ये चुम्बकीय क्षेत्र से गुजरते है तब इनमे उत्पन्न वि. वा. बल. के परिमाण के आधार पर इसका क्रम क्या होगा
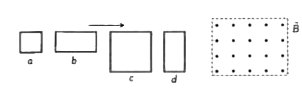
View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
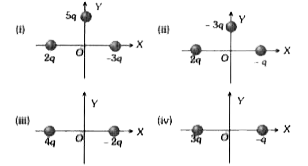
View Solutionवैनीलिन का IUPAC नाम क्या है, जिसका उपयोग आइसक्रीम में एक स्वाद उत्पन्न करने वाले कारक के रूप में किया जाता है?
View Solutionएक यौगिक (A) का उपयोग सॉल्वे प्रक्रम में अमोनिया की पुनः प्राप्ति के लिए धावन सोडा के विचरन में किया जाता है। जब CO_(2) को (A) के जलीय विखंडन में बुदबुदाया जाता है तो विलयन दूधिया हो जाता है। इसका उपयोग विसंक्रामक प्रकृति के कारण सफेदी में किया जाता है। A का रासायनिक सूत्र क्या होगा?
View Solutionसंगलित अशुद्ध धातु को लकड़ी के हरे रंग के लट्टे के साथ हिलाकर फफोलेदार तांबा को परिष्कृत किया जाता है, क्योंकि इस प्रकार की लकड़ी, हाइड्रोकार्बन गैसों (जैसे CH_4 ) को मुक्त करती है। इस प्रक्रम X को ________ कहा जाता है और इसका उपयोग धातु में प्रारंभ में उपस्थित Y की अशुद्धियों के शुद्धिकरण के लिए किया जाता है। Y _______ है।
View Solutionएक दवा तैयार करने के लिए निम्नलिखित में से किसका उपयोग किया जाता है, जिसका उपयोग एक महत्वपूर्ण विस्फोटक, RDX बनाने में भी किया जाता है?
View Solutionमैग्नीशियम के निष्कर्षण धातुकर्म में निम्नलिखित में से किस प्रक्रम का उपयोग किया जाता है?
View Solutionकैंसर के उपचार में निम्नलिखित में से किस संकुल का उपयोग किया जाता है?
View Solutionसाइक्लोहेक्सेनॉल से साइक्लोहेक्सीन के निर्माण की सबसे उत्तम विधि में किसका उपयोग किया जाता है?
View Solutionबोश प्रक्रम का उपयोग हाइड्रोजन गैस के उत्पादन के लिए किया जाता है, दी गई गैस में से किस गैस का उपयोग इसके लिए किया जाता है
View Solutionकैल्सियम के निर्माण के लिए निम्नलिखित में से किस प्रक्रम का उपयोग किया जाता है?
View Solutionएल्कीनों की असंतृप्तता के परीक्षण के लिए किस अभिकर्मक का उपयोग किया जाता है?
View Solutionनिम्नलिखित में से किस औषधि का उपयोग एक पीड़ाहारी के रूप में किया जाता है?
View Solution