एक स्थिर लिफ्ट की छत सै लटके हुए सरल लोलक का दोलनकाल T1 है। जब लिफ्ट नियत वेग सै निचे की और गति करें तो सरल लोलक का दोलनकाल T2 हो जाता है, तब
T2 अनंत
T2>T1
T2<T1
T2=T1
The correct Answer is:D
T∝1√g एवं g दोनों स्थितियों में समान है इसलिए आवर्तकाल नियत होगा।
Topper's Solved these Questions
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:Ordinary Thinking ( Objective Question) (स्प्रिंग लोलक )
Explore 50 Videos
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:Ordinary Thinking ( Objective Question) (सरल आवर्त गतियों का अध्यारोपण एवं अनुनाद )
Explore 10 Videos
- सरल आवर्त गति Book:ERRORLESS HINDIChapter:सरल आवर्त गति Exercise:Ordinary Thinking ( Objective Question) (आवर्तकाल एवं आवृति )
Explore 22 Videos
- विधुत चुम्बकीय प्रेरण Book:ERRORLESS HINDIChapter:विधुत चुम्बकीय प्रेरण Exercise:Self Evaluation Test विधुत चुम्बकीय प्रेरण
Explore 17 Videos
- स्थिर वैद्युतBook:ERRORLESS HINDIChapter:स्थिर वैद्युतExercise:Self Evaluation Test
Explore 8 Videos
Similar Questions
बराबर द्रव्यमान के दो पिंड M तथा N दो द्र्व्यमाहीन स्प्रिंगों से अलग-अलग लटके है। स्प्रिंगों के बल नियतांक क्रमशः k1 तथा k2 है। यदि दोनों पिंड उर्ध्वाधर तल में इस प्रकार कम्पन्न करते है की इनके अधिकतम वेग बराबर है , तब म के कम्पन के आयाम का N के साथ अनुपात है।
View Solutionदो सरल आवर्त गतियां निम्न समीकरण द्वारा प्रदर्शित है
y1=5(sin2πt+√3cos2πt) तथा y2=5sin(2πt+π4)
इन दोनों के आयामों का अनुपात होगा।
View Solutionकोई कण इस प्रकार गति करता है की उसका त्वरण समीकरण a = -bx द्वारा प्रदर्शित किया जाता है , जिसमें x संतुलन स्थिति से विस्थापन तथा b कोई नियतांक है। दोलनकाल होगा।
View Solutionचित्र में चार तार लूपो को दिखाया गया है। जिनकी भुजाओ की लम्बाई L या 2L है सभी चारो एकसमान वेग से एक समरूप चुम्बकीय क्षेत्र →B (कागज़ तल के लम्बवत बाहर की ओर) से गुजरते है। जब ये चुम्बकीय क्षेत्र से गुजरते है तब इनमे उत्पन्न वि. वा. बल. के परिमाण के आधार पर इसका क्रम क्या होगा
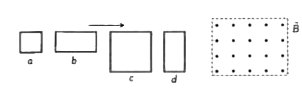
View Solutionनिम्न चार स्थितियों में आवेशित कण मूल बिंदु से बराबर - बराबर दूरियों पर स्थित हैं मूल बिंदु क्षेत्र के परिमाण को अधिकतम पहले लेते हुये इन्हें व्यवस्थित करें
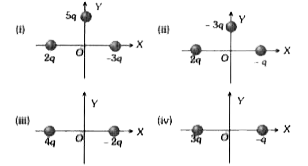
View Solutionदोलन|सरल आवर्त गति #!# सरल आवर्त गति का वेग समीकरण
View Solutionसरल लोलक तथा सेकंड लोलक
View Solutionपृथ्वी की त्रिज्या के तुलनीय लंबाई के सरल लोलक का आवर्तकाल|मुक्त दोलन तथा अवमंदित दोलन
View Solutionदोलन |सरल आवर्त गति #!#कोणीय सरल आवर्त गति #!#सरल लोलक
View Solutionदोलन|सरल आवर्त गति #!#सरल लोलक के प्रकार
View Solutionदोलन|सरल आवर्त गति #!#सरल लोलक के नियम
View Solutionसरल लोलक
View Solutionद्वितीयक लोलक, सरल लोलक की सहायता से g का मान ज्ञात करना
View Solutionसरल आवर्त गति में ऊर्जा|सरल लोलक
View Solutionसरल आवर्त गति पर महत्वपूर्ण प्रश्न|सरल लोलक विभिन्न स्थितियों में
View Solutionसरल लोलक की गति तथा महत्वपूर्ण प्रश्न
View Solution

