An equation of the XOY plane is
A
x=0
B
y=0
C
z=0
D
z=c,c≠0
Video Solution
Text Solution
The correct Answer is:C
|
Answer
Step by step video, text & image solution for An equation of the XOY plane is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THE DIMENSIONAL GEOMETRY BOOK - MCGROW HILL PUBLICATIONCHAPTER - THE DIMENSIONAL GEOMETRY EXERCISE - EXERCISE (LEVEL 2 (SINGLE CORRECT ANSWER TYPE QUESTIONS))
16 Videos
- THE DIMENSIONAL GEOMETRY BOOK - MCGROW HILL PUBLICATIONCHAPTER - THE DIMENSIONAL GEOMETRY EXERCISE - EXERCISE (NUMERICAL ANSWER TYPE QUESTIONS)
20 Videos
- THE DIMENSIONAL GEOMETRY BOOK - MCGROW HILL PUBLICATIONCHAPTER - THE DIMENSIONAL GEOMETRY EXERCISE - EXERCISE (CONCEPT-BASED (SINGLE CORRECT ANSWER TYPE QUESTIONS ))
15 Videos
- STATISTICS BOOK - MCGROW HILL PUBLICATIONCHAPTER - STATISTICS EXERCISE - QUESTION FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPERS
13 Videos
- TRIGONOMETRICAL IDENTITIES AND EQUATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - TRIGONOMETRICAL IDENTITIES AND EQUATIONS EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
20 Videos
Similar Questions
Knowledge Check
A plane meets the co-ordinate axes at A,B,C and (α,β,γ) is the centroid of the triangle ABC. Then the equation of the plane is
Aαx+βy+γz=1Bxα+yβ+zγ=1Cxα+yβ+zγ=3D3xα+3yβ+3zγ=1A plane meets the co-ordinate axes in A,B,C, such that the centroid of △ABC is (3,3,3). Then the equation of the plane is
Ax+y+z=3Bx+y+z=9C3x+3y +3z=1D9x+9y + 9z=1If the foot of the perpendicular from the origin to a plane is (2,-3,4), then the equation of the plane is
A2x+3y+4z=29B2x+3y-4z=29C2x-3y+4z+29D2x-3y-4z=29
Find the equation of the plane with intercept 3 on the y-axis and parallel to ZOX plane.
View SolutionWrite the equation of the plane passing through (a , b , c) and parallel to xy-plane
View SolutionMatch the equation of the plane in column I and columa II
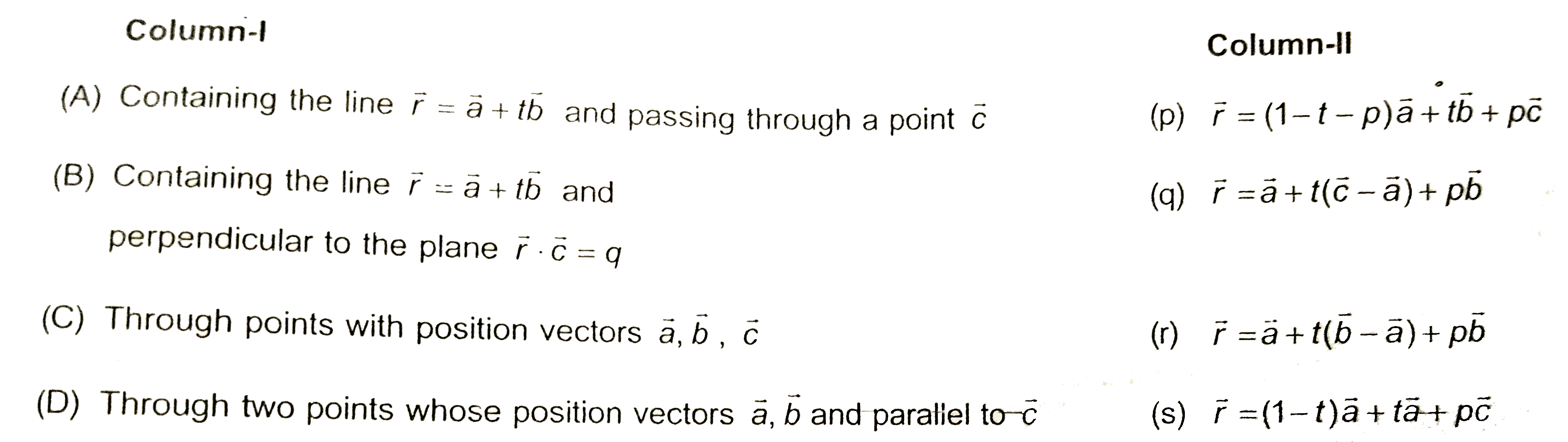
View SolutionLet P(-7,1,-5) be a point on a plane and let O be the origin. If OP is normal to the plane, then the equation of the plane is
View SolutionLet N be the foot of the perpendicular of length p from the origin to a plane and l, m, n be the direction cosines of ON, the equation of the plane is
View Solution

