The circle passing through (t,1),(1,t)and(t,t) for all values of t also passes through
(1,−1)
(−1,1)
(−1,−1)
(1,1)
The correct Answer is:D
Step by step video, text & image solution for The circle passing through (t,1), (1,t) and (t,t) for all values of t also passes through by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLES AND SYSTEMS OF CIRCLES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CIRCLES AND SYSTEMS OF CIRCLES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. AIEEE/JEE MAIN PAPERS
56 Videos
- CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES BOOK - MCGROW HILL PUBLICATIONCHAPTER - CARTESIAN SYSTEM OF RECTANGULAR COORDINATES AND STRAIGHT LINES EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B - ARCHITECTURE (ENTRANCE EXAMINATION PAPERS)
14 Videos
- COMPLEX NUMBERS BOOK - MCGROW HILL PUBLICATIONCHAPTER - COMPLEX NUMBERS EXERCISE - QUESTIONS FROM PREVIOUS YEARS. B-ARCHITECTURE ENTRANCE EXAMINATION PAPER
17 Videos
Similar Questions
The circle passing through the distinct points (1,t),(t1) & (t,t) for all real values of t,passes through the point (a.b),then a2+b2 is?
View SolutionCalculate the amount of current passing through a wire at t=9 s, if the electric charge passing through a cross section of wire in t time is given as q(t)=7t2+9t−2.
View Solution
Knowledge Check
Find the current passing through battery at t=0 and t=∞
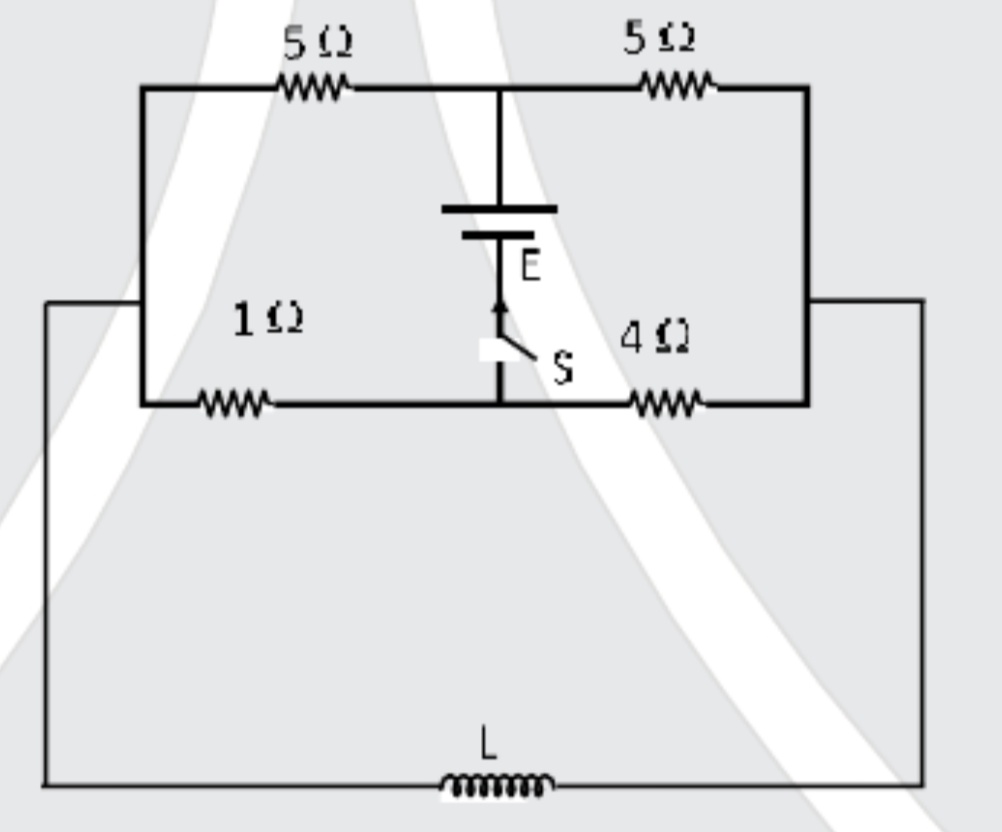 A(518)E,(1033)EB(1018)E,(533)EC(59)E,(1013)ED(510)E,(2033)E
A(518)E,(1033)EB(1018)E,(533)EC(59)E,(1013)ED(510)E,(2033)ELet C be the circle x2+y2=1 in the xy-plane . For each t≥0, let Lt be the line passing through (0,1) and (t,0) . Note than Lt interesects C in two points, one of which is (0,1). Let Qt be the other point. As t varies between 1 and 1+√2 , the collection of points Q1 sweeps out an arc on C. The angle subtended by this arc at (0,0) is
Aπ8Bπ4Cπ3D3π8A particle moves in a straight line with a constant acceleration. It passing through a distance 135 m in t second. The value of t (in second) is
A12B9C10D1.8
If t1andt2 are roots of eth equation t2+λt+1=0, where λ is an arbitrary constant. Then prove that the line joining the points (at1,22at1)and(at2,22at2) always passes through a fixed point. Also, find the point.
View SolutionIf t1 and t2 are roots of the equation t2+λt+1=0 where λ is an arbitrary constant. Then the line joining the points ((at1)2,2at1) and (a(t2)2,2at2) always passes through a fixed point then find that point.
View SolutionA parabola with vertex (2, 0) and axis of symmetry parallel to the y-axis, passes through (3, 1) and (−3,t), then the value of t is. 30 (b) 35 (c) 20 (d) 25
View SolutionLet ABCD be a square of side length 2 units. C2 is the circle through vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A
A line M through A is drawn parallel to BD. Point S moves such that its distances from the line BD and the vertex A are equal. If locus of S cuts. M at T2 and T3 and AC at T1, then area of ΔT1T2T3 is
View SolutionIf f(t)=1−t1+t then the value of f'(1/t) is
View Solution
