यदिax=by=cx=du तथा a b c d गुणोत्तर श्रेणी में हो तब x y z u होंगे
समान्तर श्रेणी में
गुणोत्तर श्रेणी में
हरात्मक श्रेणी में
इनमे से कोई नहीं
The correct Answer is:C
Step by step video, text & image solution for यदिa^x=b^y=c^x=d^u तथा a b c d गुणोत्तर श्रेणी में हो तब x y z u होंगे by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- श्रेणियाँ Book:ERRORLESS HINDIChapter:श्रेणियाँ Exercise:SOLVED MULTIPLE CHOICE QUESTIONS (समान्तरीय गुणोत्तर श्रेणी अंतर विधि)
Explore 3 Videos
- श्रेणियाँ Book:ERRORLESS HINDIChapter:श्रेणियाँ Exercise:SOLVED MULTIPLE CHOICE QUESTIONS (n वें पदों की विशेष श्रेणियाँ, n पदों का योग और अनन्त पदों का योग)
Explore 22 Videos
- श्रेणियाँ Book:ERRORLESS HINDIChapter:श्रेणियाँ Exercise:SOLVED MULTIPLE CHOICE QUESTIONS (हरात्मक श्रेणी)
Explore 6 Videos
- शांकव परिच्छेद Book:ERRORLESS HINDIChapter:शांकव परिच्छेद Exercise:JEE Advanced (Matrix Match type questions)
Explore 7 Videos
- सदिश बीजगणित Book:ERRORLESS HINDIChapter:सदिश बीजगणित Exercise:JEE Advanced (Matrix Match type questions)
Explore 7 Videos
Similar Questions
श्रेणी 1+4x+7x2+10x3+….∞का योग होगा |
View Solutionश्रेणी 1+(1+3)+(1+3+5)+…..के (n-1)पदों का योग होगा
View Solution13 15 19 में क्या जोड़े की योग से प्राप्त पद हरात्मक श्रेणी के कर्मगत पद है
View Solution
View Solution
View SolutionIf a,b,c,d are in GP and a^(x)=b^(x)=c^(z)=d^(u) then x,y,z,u are in
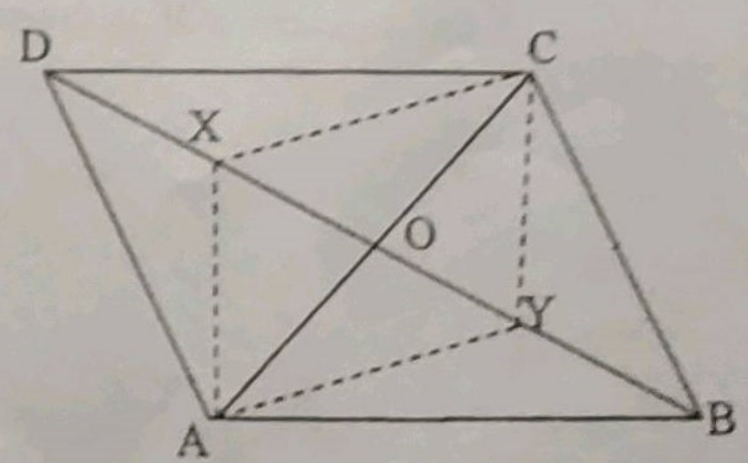
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View Solution(x−y)(1−dydx)=ey, where x−y=u A)ueu−eu=ex+c B)u2=ex+c C)u2=12ex+c D)u2ex=2x+c
View SolutionIf a^(x) = b^(y) = c^(z) = d^(t) and a ,b ,c d are in G.P . Then x, y, z, t are in
View Solutionयदि a,b,c,d गुणोत्तर श्रेढी में हों, तो सिद्ध कीजिए कि :
(b+c)(b+d)=(c+a)(c+d)
View Solutionयदि a,b,c समान्तर और a,b,c+1 गुणोत्तर श्रेणी में हो तो
View Solutionयदि 16sin2θ,cosθ तथा secθ गुणोत्तर श्रेणी में हो, तब θ समान होगा (n∈Z)
View Solutiona^(x) = b^(y) = c^(z) = d^(t) and a,b,c,d are in G.P. , then x,y,z,t are in :
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
View SolutionIf u=x−acandv=y−bd then bxy=
View SolutionIf a,b,c,d are in GP and ax=by=cz=du, then x,y,z,u are in
View Solution

