Suppose n students appear in an examination. Let X = the number of students who pass the examination. Suppose P(X=k)=λk2, then value of λ is
2n(n+1)
6n(n+1)(2n+1)
4n2(n+1)2
2n+1n2(n+1)2
The correct Answer is:B
To solve the problem, we need to find the value of λ given the probability distribution of the number of students passing the examination. The probability that X=k is given as P(X=k)=λk2.
1. Understanding the Probability Distribution:
We know that P(X=k)=λk2 for k=0,1,2,…,n. The total probability must sum to 1:
n∑k=0P(X=k)=1
2. Writing the Total Probability:
We can express the total probability as:
n∑k=0P(X=k)=n∑k=0λk2=λn∑k=0k2
3. Calculating the Sum of Squares:
The sum of squares of the first n natural numbers is given by the formula:
n∑k=1k2=n(n+1)(2n+1)6
Note that n∑k=0k2=02+n∑k=1k2=0+n(n+1)(2n+1)6.
4. Setting Up the Equation:
We can now set up the equation:
λ⋅n(n+1)(2n+1)6=1
5. Solving for λ:
Rearranging the equation gives:
λ=6n(n+1)(2n+1)
Final Answer:
Thus, the value of λ is:
λ=6n(n+1)(2n+1)
We know that P(X=k)=λk2 for k=0,1,2,…,n. The total probability must sum to 1:
n∑k=0P(X=k)=1
We can express the total probability as:
n∑k=0P(X=k)=n∑k=0λk2=λn∑k=0k2
The sum of squares of the first n natural numbers is given by the formula:
n∑k=1k2=n(n+1)(2n+1)6
Note that n∑k=0k2=02+n∑k=1k2=0+n(n+1)(2n+1)6.
We can now set up the equation:
λ⋅n(n+1)(2n+1)6=1
Rearranging the equation gives:
λ=6n(n+1)(2n+1)
Thus, the value of λ is:
λ=6n(n+1)(2n+1)
Topper's Solved these Questions
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Exercises (Level 2 Single Correct Answer)
12 Videos
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Exercises (Numerical Answer)
28 Videos
- PROBABILITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Exercises (Single Correct Answer)
10 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - MCGROW HILL PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
17 Videos
- PROGRESSIONSBOOK - MCGROW HILL PUBLICATIONCHAPTER - PROGRESSIONSEXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
25 Videos
Similar Questions
Express the following ratios in the language of daily life: In an examination, the ratio of the number of students passing the examination to the total number of students that appeared in the examination is 4:5. Water is formed by combining volumes of oxygen and hydrogen in the ratio 1:2. To dilute an acid, students were asked to mix acid and water in the ratio 2:3.
View Solution100 students appeared in annual exami-nation. 60 students passed. The ratio of the number of students who failed to the total number of students is
View Solution
Knowledge Check
Study the following table and answer question.
Number of students appeared in an examination from five citie s:
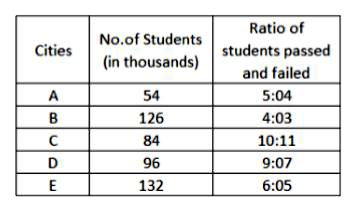
The total number of students who appeared in the examination from cities C and D is what percent more than the total number of students who failed in cities A, B and E ? (nearest to an integer)A44B30C41D42Study the following table and answer question.
Number of students appeared in an examination from five cities :
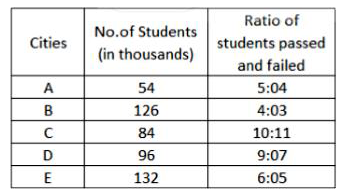
The ratio of the total number of students passed in the examination from cities A and D to that of students failed from cities B and E ?A9:16B5:9C13:18D14:19In a class among the passed students Nitu is 22nd from the top and Aparna, who is 5 ranks below Nitu is 34th from the bottom. All the students from the class appeared for an examination. If the ratio of the students who passed in the examination to those who failed is 4:1 for the class, how many students were there in the class?
AData inadequateB75C60DNone of these
2,71,855 students appeared at an examination. Out of them 1,27,968 failed. How many students passed ?
View SolutionIn an examination, 30% and 35% students respectively failed in History and Geography while 27% students failed in both the subjects. If the number of students passing the examination is 248, find the total number of students who appeared in the examination. 380 b. 400 c. 425 d. 725
View SolutionThe given graph shows the marks obtained by students in an examination.
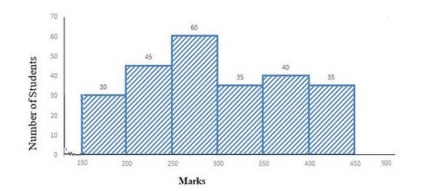 The number of students who obtained less than 300 marks is what percent more than the number of students who obtained 350 or more marks?
The number of students who obtained less than 300 marks is what percent more than the number of students who obtained 350 or more marks?
View Solution75% of the students passed in an examination. If 2 more students had passed the examination. 80% would have been successful. How many students are there in the class?
View SolutionThe average marks obtained by 140 students in an examination is 90. If the average marks of passed students is 120 and the number of students who failed the examination are 90, then what is the average marks of students who failed the examination?
View Solution
