Fig. 24.8 shows three events A, B and C. Probabilities of different ev

Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
$P (A \cap B' \cap C')$ =0.18 , $P (A' \cap B \cap C')$ = 0.06 etc.

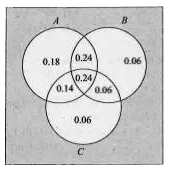
Which of the following is not true ?
AA and B are independent
BB and C are independent
CA and C are independent
DA and $B \cap C$ are independent
Let $A, B$ and $C$ be sets such that $A \cap B \subseteq C$ and $A \cap B \neq ϕ$ . Then which of the following statements is not true?
A $B \cap C \neq ϕ$
BIf $(A - B) \subseteq C$ , then $A \subseteq C$
C $C (\cup A) \cap (C \cup B) = C$
DIf $(A - C) \subseteq B$ , then $A \subseteq B$
For two given events A and B $P (A \cap B)$ =
ANot less than P(A) + P(B) -1
BNot greater than P(A) + P(B)
CEqual to $P (A) + P (B) - P (A \cup B)$
DAll of the above

Fig. 24.8 shows three events A, B and C. Probabilities of different events are shown in the figure. For instance,
$P (A \cap B' \cap C')$ =0.18 , $P (A' \cap B \cap C')$ = 0.06 etc.

Which of the following is not true ?