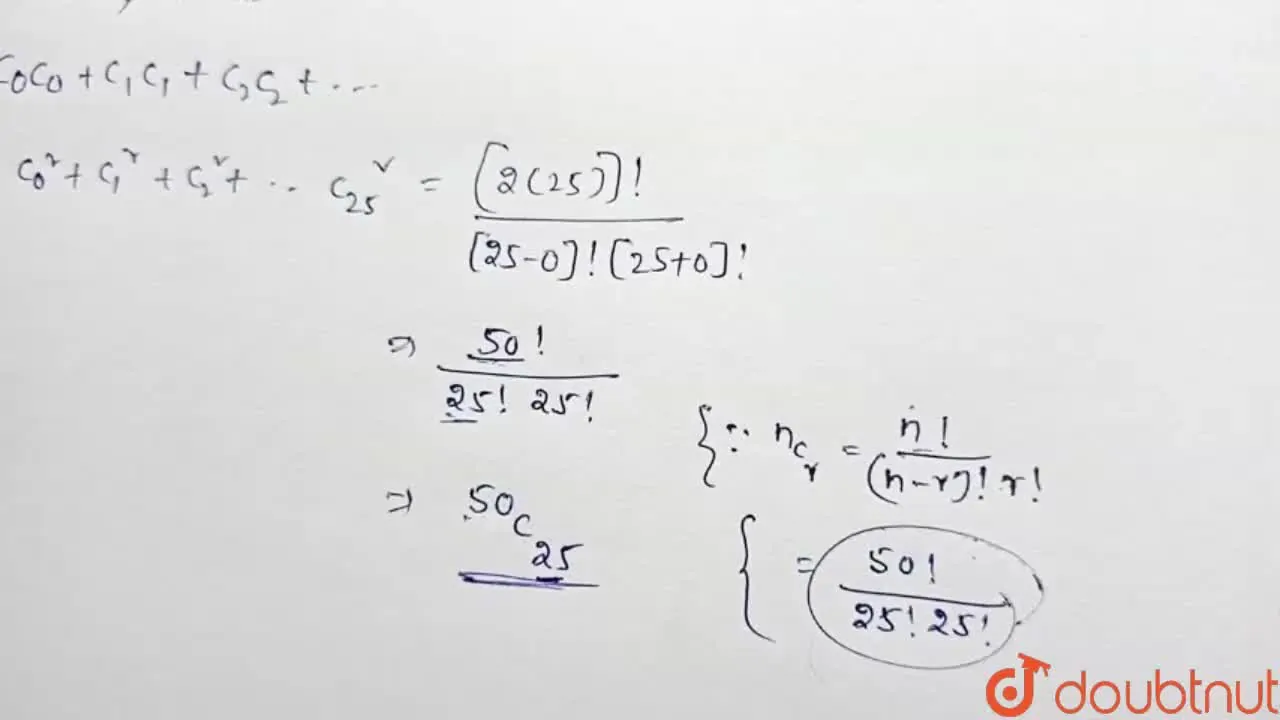C20+C21+C22+………+C225 = Solution in Telugu
49C50
49C25
50C25
39C40
The correct Answer is:C
Step by step video, text & image solution for C_0^2 + C_1^2 + C_2^2 + ………+C_25^2 = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - AAKASH SERIESCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE - II109videos
BINOMIAL THEOREM
- BOOK - AAKASH SERIESCHAPTER - BINOMIAL THEOREMEXERCISE - PRACTICE EXERCISE95videos
BINOMIAL THEOREM
- BOOK - AAKASH SERIESCHAPTER - BINOMIAL THEOREMEXERCISE - ADDITIONAL EXERCISE25videos
BINOMIAL THEOREM
- BOOK - AAKASH SERIESCHAPTER - AREASEXERCISE - Exercise-3.221videos
AREAS
- BOOK - AAKASH SERIESCHAPTER - CIRCLEEXERCISE - EXERCISE -1.438videos
CIRCLE
Similar Questions
If rth term is middle term in (x2−12x)20 then (r+3)th term is
03:47View SolutionThe middle term in the expansion of (x+1x)2n is
11:58View SolutionThe term independent of x (x>0,x≠1) in the expansion of [(x+1)(x2/3−x1/3+1)−(x−1)(x−√x)]10 is
03:17View SolutionFind the area of the region bonded by y=x(x−1)(x−2), the x-axis and x = 0 and x = 4.
View SolutionDiscuss the relative position of the fol-
lowing pair of circles.
x2+y2−4x−6y−12=0
x2+y2+6x+18y+26=0.02:35View SolutionIf C0,C1,C2,....,Cn are coefficients in the binomial expansion of (1+x)n and n is even, then C20−C21+C22−C23+...+(−1)C2n, is equal to
05:15View SolutionIf .25C0+5.25C1+9.25C2....101.25C25=225k find k = ?
03:12View SolutionIf (1+x)n=C0+C1x+C2x2+….....+Cnxn, then C0+2.C1+3.C2+….+(n+1).Cn=
01:37View SolutionC02+C13+C24+…...+Cnn+2=
08:58View Solution(1+x)n=c0+c1x+c2x2+...+Cnxn
হলে দেখাও যে,(c0+c1+c2+...+cn)2=2nc0+2nc1+2nc2+...+2nc2n02:26View SolutionShow that C0+(C0+C1)+(C0+C1+C2)+…….+
(C0+C1+…+Cn)=(n+2).2n−101:34View SolutionC0+2.C1+4.C2+…….+Cn.2n=243 , then n =
05:04View SolutionC20+C21+C22−………−C215 =
03:32View SolutionIf .25C0+5.25C1+9.25C2....101.25C25=225k find k = ?
03:51View SolutionIf C01+C12+C23=0 , where C0C1,C2 are all real, the equation C2x2+C1x+C0=0 has
06:09View SolutionIfC0,C1,C2..Cn denote the coefficients in the binomial expansion of (1+x)n, then C0+2.C1+3.C2+.(n+1)Cn
08:44View Solution