R त्रिज्या के किसी एकसमान आवेशित ठोस गोले के पृष्ठ का विभव है। ( के सापेक्ष मापा गया)। यदि इस गोले के लिए, तथा विभवों वाले समविभवी पृष्ठों की त्रिज्यायें, क्रमशः , तथा है, तो
तथा
तथा
तथा
The correct Answer is:C, D
आवेशित गोले की सतह पर विभव
तथा
बाह्य बिन्दु के लिए विभव घटता है।
प्रश्नानुसार,
या
या
या
इसी प्रकार,
या
या
अतः विकल्प (b) और (c ) दोनों सही है।
Topper's Solved these Questions
Similar Questions
एक प्रेक्षक प्रकाश गति की आधी गति से 10 GHz आवृत्ति के एक स्थिर सूक्ष्म तरंग (microwave) स्रोत की तरफ जा रहा है। प्रेक्षक द्वारा मापी गयी सूक्ष्म तरंग की आवृत्ति का मान होगा। (प्रकाश की चाल =3×108ms−1)।
View Solutionएक घन की तीन भुजाओं तथा द्रव्यमान के मापन द्वारा घन के पदार्थ का घनत्व ज्ञात किया जाता है यदि द्रव्यमान तथा लम्बाई में आपेक्षित प्रतिशत त्रुटि क्रमशः 1.5% तथा 1% है तो घनत्व में अधिकतम त्रुटि होगी
View SolutionA uniformly charged solid shpere fo radius R has potential V0 (measured with respect to ∞) on its surface. For this sphere the equipotentail surfaces with potentials 3V02,5V04,3V04 and V04 have radius R1,R2,R3 and R4 respecatively. Then
View Solutionकिसी त्रिभुज के शीर्षो के निर्देशांक (2,5),(6−2) तथा (−3,−4) है , तो उसकी मध्यिकाओ के समीकरण ज्ञात कीजिए
View SolutionR त्रिज्या के किसी एकसमान आवेशित ठोस गोले के पृष्ठ का विभव V0 है (∞ के सापेक्ष मापा गया)। इस गोले के लिए, 3V02,5V04,3V04 तथा V04 विभवों वाले समविभवी पृष्ठों की त्रिज्याएँ, क्रमशः R1,R2,R3 तथा R4 हैं, तो
View Solutionत्रिज्या r तथा ऊँचाई h वाले बेलन के लिए त्रिज्या के सापेक्ष पृष्ठीय क्षेत्रफल में परिवर्तन की दर ज्ञात करो।
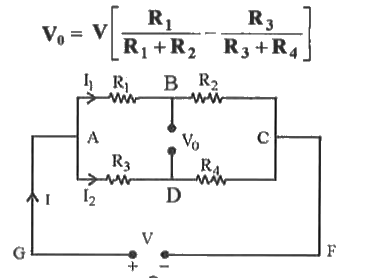
View Solutionचित्र में प्रदर्शित जाल के लिये किरचॉफ के नियमों का उपयोग कर सिद्ध कीजिये कि
V0=V[R1R1+R2−R3R3+R4]
View Solutionयदि बिन्दु (4, 2) का रेखा L = 0 के सापेक्ष प्रतिबिम्ब (-2, 6) है, तो L का समीकरण है
View Solutionएक फलन g जो प्रत्येक वास्तविक संख्या x>0 के लिए परिभाषित है तथा g(1)=1,g'(x2)=x3 को सभी x>0 के लिए सन्तुष्ट करता है, तो g (4) का मान है
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionयदि किसी गोले का समीकरण x2+y2+z2+2ux+2vy+2wz+d=0 है, तो गोले के केन्द्र का निर्देशांक तथा त्रिज्या क्या होगी?
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View Solutionयदि गोले का सदिश समीकरण, →r2−→r.(8ˆi−6ˆj+10ˆk)−50=0 है, तो गोले के केन्द्र के निर्देशांक और त्रिज्या ज्ञात कीजिए।
View SolutionA uniformly charged solid sphere of radius R has potential V0 (measured with respect to ∞) on its surface. For this sphere the equipotential surfaces with potentials 3V02,5V04,3V04 and V04 have radius R1,R2,R3 and R4 respecatively. Then
View SolutionThe radius of a sphere is equal to the base radius and height of a right circular cylinder. What is the ratio between the surface area of the sphere and curved surface area of the cylinder ?
किसी गोले की त्रिज्या, एक लंबवत बेलन (सिलिंडर) के आधार की त्रिज्या तथा ऊंचाई के बराबर है | गोले की पृष्ठभूमि क्षेत्रफल (सरफेस एरिया) तथा बेलन (सिलिंडर) के वक्र पृष्ठ के क्षेत्रफल का अनुपात कितना है ?
View Solution
