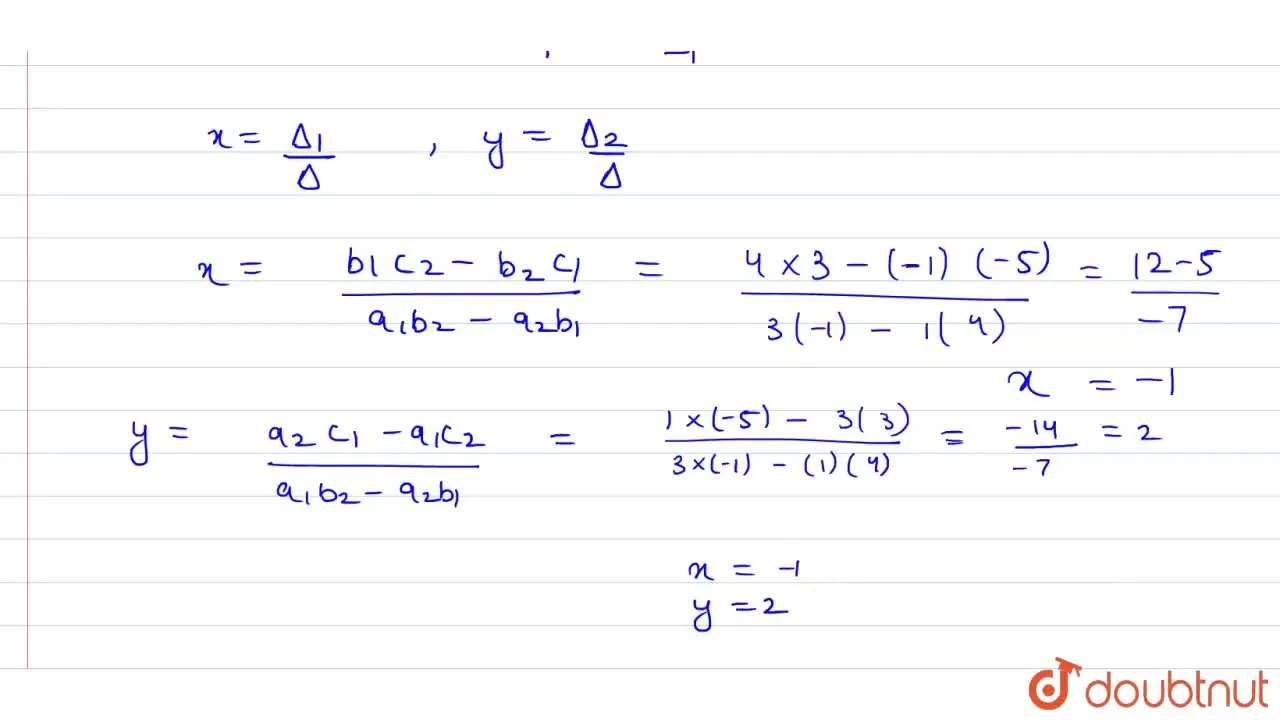3x+4y-5=0
x-y+3=0
The correct Answer is:x=-1 y=2
Step by step video, text & image solution for 3x+4y-5=0 x-y+3=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - SYSTEM OF LINEAR EQUATIONSEXERCISE - EXERCISE 8A (USING MATRICES ,SOLVE THE FOLLOWING SYSTEM OF EQUATIONS.)2videos
SYSTEM OF LINEAR EQUATIONS
- BOOK - RS AGGARWALCHAPTER - SYSTEM OF LINEAR EQUATIONSEXERCISE - EXERCISE 8A (VALUE BASED QUESTIONS)4videos
SYSTEM OF LINEAR EQUATIONS
- BOOK - RS AGGARWALCHAPTER - SYSTEM OF LINEAR EQUATIONSEXERCISE - Objective Questions53videos
SYSTEM OF LINEAR EQUATIONS
- BOOK - RS AGGARWALCHAPTER - STRAIGHT LINE IN SPACEEXERCISE - Objective Questions19videos
STRAIGHT LINE IN SPACE
- BOOK - RS AGGARWALCHAPTER - THE PLANEEXERCISE - Objective Questions35videos
THE PLANE
Similar Questions
Determine the nature of the quadrilateral formed by four lines 3x+4y−5=0,4x−3y−5=0;3x+4y−5=0and4x−3y+5=0 Find the equation of the circle insc quadrilateral inscribed and circumscribing this quadrilateral.
View SolutionThe equaiton of the lines representing the sides of a triangle are 3x−4y=0,x+y=0 and 2x - 3y = 7 . The line 3x + 2y = 0 always passes through the
View SolutionIf OAandOB are equal perpendicular chords of the circles x2+y2−2x+4y=0 , then the equations of OAandOB are, where O is the origin. 3x+y=0 and 3x−y=0 3x+y=0 and 3y−x=0 x+3y=0 and y−3x=0 x+y=0 and x−y=0
View SolutionFind the equation of the bisectors of the internal angles of the triangle whose sides are :
3x+4y−6=0 , 12x−5y−3=0, 4x−3y+12=0View Solution26 Which of the following lines have the intercepts of equal lengths on the circle, x2+y2−2x+4y=0 (A) 3x−y=0 (B) x+3y=0(C) x+3y+10=0 (D) 3x−y−10=0
View SolutionFind the distance between the parallel lines 4x-3y+5=0 and 4x-3y=0
View SolutionTwo sides of a rectangle are 3x+4y+5=0, 4x-3y+15=0 and one of its vertices is (0, 0). The area of rectangle is ___.
View SolutionThe perimeter of a parallelogram whose sides are represented by the lines x+2y+3=0,
3x+4y−5=0,2x+5=0and3x+4y−10=0 is equal toView SolutionGiven the four lines with the equations
x+2y−3=0, 3x+4y−7=0,
2x+3y−4=0, 4x+5y−6=0, thenView SolutionShow that the lines 3x−4y+5=0,7x−8y+5=0and4x+5y=45 are concurrent.
View Solution