In the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : (i)AB+CQ=AC+BQ
(ii) Area (△ABC)=12(Perimeter of△ABC)×r
We know that the lengths of tangents from an exterior point to a circle are equal.
∴AP=AR, ……….(i) [tangents from A]
BP=BQ, ………(ii) [tangents from B]
CQ=CR ………….(iii) [tangents from C]
(a)AB+CQ=AP+BP+CQ
=AR+BQ+CR [using (i), (ii) and (iii)]
=(AR+CR)+BQ=AC+BQ.
(b) Join OA, OB and OC.
Area (ΔABC)=area(ΔOAB)+area(ΔOBC)+area(ΔOCA)
=(12×AB×OP)+(12×BC×OQ)+(12×CA×OR)
=(12×AB×r)+(12×BC×r)+(12×CA×r)
=12(AB+BC+CA)×r
=12(perimeter ofΔABC)×r.

Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
The sides AB,BC and AC of a triangle ABC touch a circle with centre O and radius r at P, Q, and R respectively.
View Solution25. In figure, the sides AB, BC and CA of triangle ABC touch a circle with centre and radius r at P, Q and R respectively. Prove that (i ) AB+CQ=AC+BQ (ii) Area ΔABC=12 perimeter of ΔABC).r.
View Solution
Knowledge Check
In figure , the sides AB, BC and CA of triangle ABC, touch a circle at P,Q and R, respectively . If PA = 4 cm , BP = 3 cm and AC = 11 cm , then length of BC is
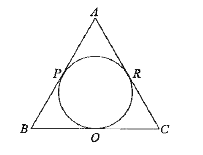 A11 cmB15 cmC14 cmD10 cm
A11 cmB15 cmC14 cmD10 cmIn the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
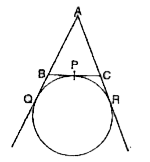 AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC
AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC
In Fig. 10.20, the sides AB, BC and CA of triangle ABC touch a circle with centre O and radius r at P, Q and R respectively. (FIGURE) Prove that: 1) AB + CQ = AC + BQ 2) Area (ABC) = (r/2)*(Perimeter of ABC)
View SolutionThe side AB, BC and CA of triangle ABC touch a circle at P,Q and R respectively. If PA =4 cm, BP=3 cm and AC=11 cm, then length of BC is

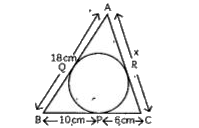
View SolutionIn the figure, all three sides of a triangle ABC touch the circle at points P, Q and R. Find the value of x.
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionA circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View Solution
