A circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter ofΔABC).
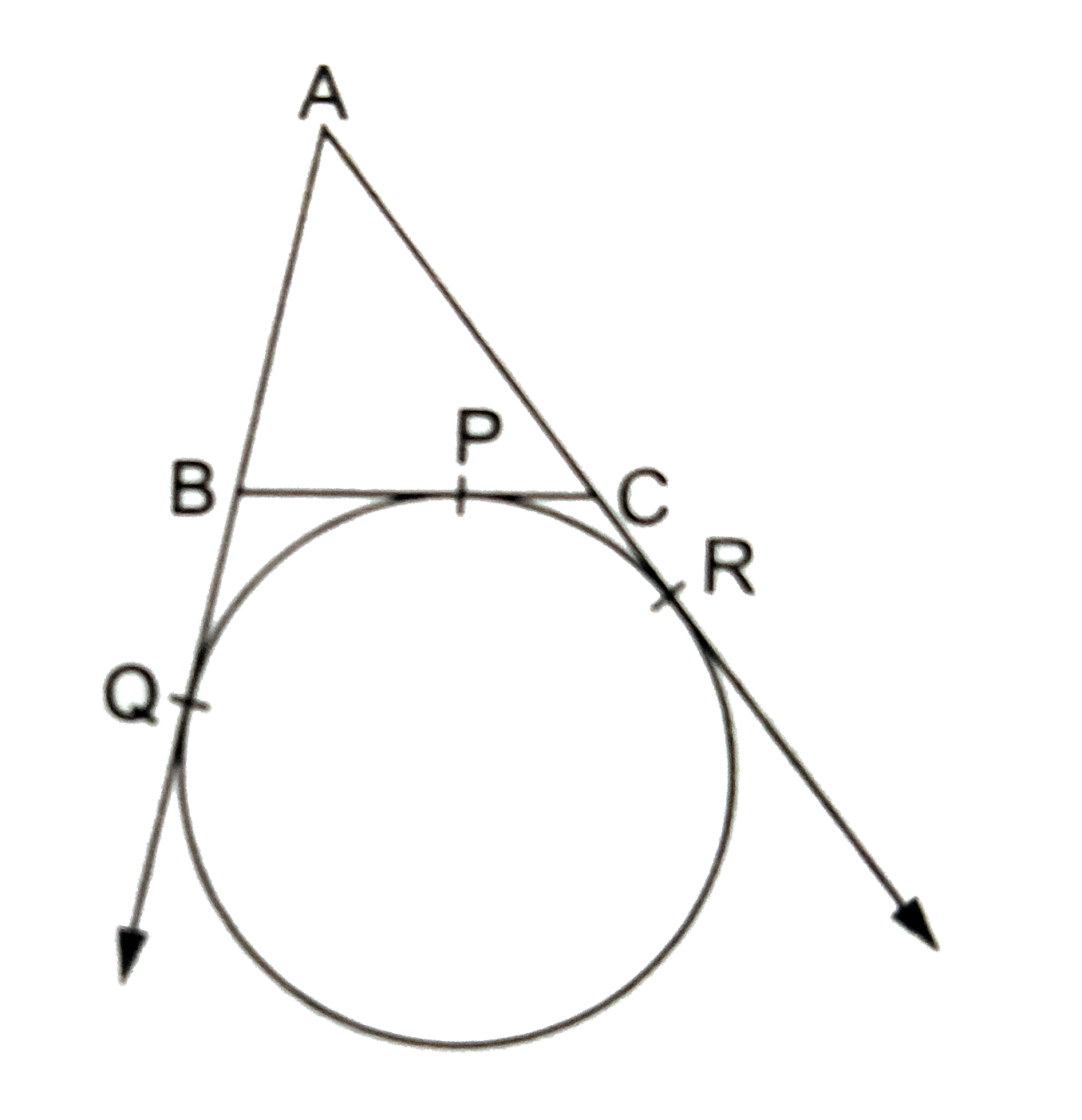
We know that the lengths of tangents drawn from an external point to a circle are equal.
∴AQ=AR, ……….(i) [tangents from A]
BP=BQ, ………..(ii) [tangents from B]
CP=CR. ………..(iii) [tangents from C]
Perimeter of ΔABC
=AB+BC+AC
=AB+BP+CP+AC
=AB+BQ+CR+AC [using (ii) and (iii)]
=AQ+AR
=2AQ[ using (i) ]
∴AQ=12(perimeter ofΔABC).
Topper's Solved these Questions
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8A
16 Videos
- CIRCLESBOOK - RS AGGARWALCHAPTER - CIRCLESEXERCISE - Exercise 8B
15 Videos
- ARITHMETIC PROGRESSIONBOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Multiple Choice Questions (Mcq)
30 Videos
- CONSTRUCTIONSBOOK - RS AGGARWALCHAPTER - CONSTRUCTIONSEXERCISE - Test Yourself
10 Videos
Similar Questions
A circle is touching the side BC of ΔABC at P and touching AB and AC produced at Q and R respectively Prove that AQ=12(Perimeter of ΔABC)
View SolutionA circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
View Solution
Knowledge Check
A circle touches the side BC of a ΔABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of ΔABC = 26.4 cm, then the length of AQ is:
A8.8 cmB13.2 cmC15.4 cmD17.6 cmIn the figure shown here, a circle touches the side BC of a triangle ABC at P and AB and AC produced at Q and R respectively. What is AQ equal to ?
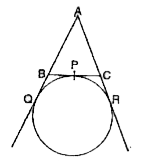 AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABC
AOne-third of the perimeter of Δ ABC.BHalf of the perimeter of Δ ABC.CTwo-third of the perimeter of Δ ABCDThree-fourth of the perimeter of Δ ABCA circle touches the side BC of ΔABC at D and AB and aC are produced to E and F, respectively. If AB=10cm, AC=8.6 cm and BC=6.4 cm then BE=?
A3.5cmB3.2cmC2.5cmD2.2cm
A circle is touching the side BC of ABC at P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(Perimeter of ABC) .
View SolutionA circle touches the side BC of ΔABC at P and touches AB and AC produced at Q and R respectively. Prove that AQ=1/2(Perimeter of ΔABC).
View SolutionA circle touches the side BC of ΔABC at F and touches AB and AC at D and E, respectively. If AD = 8 cm, then find the perimeter of ΔABC.

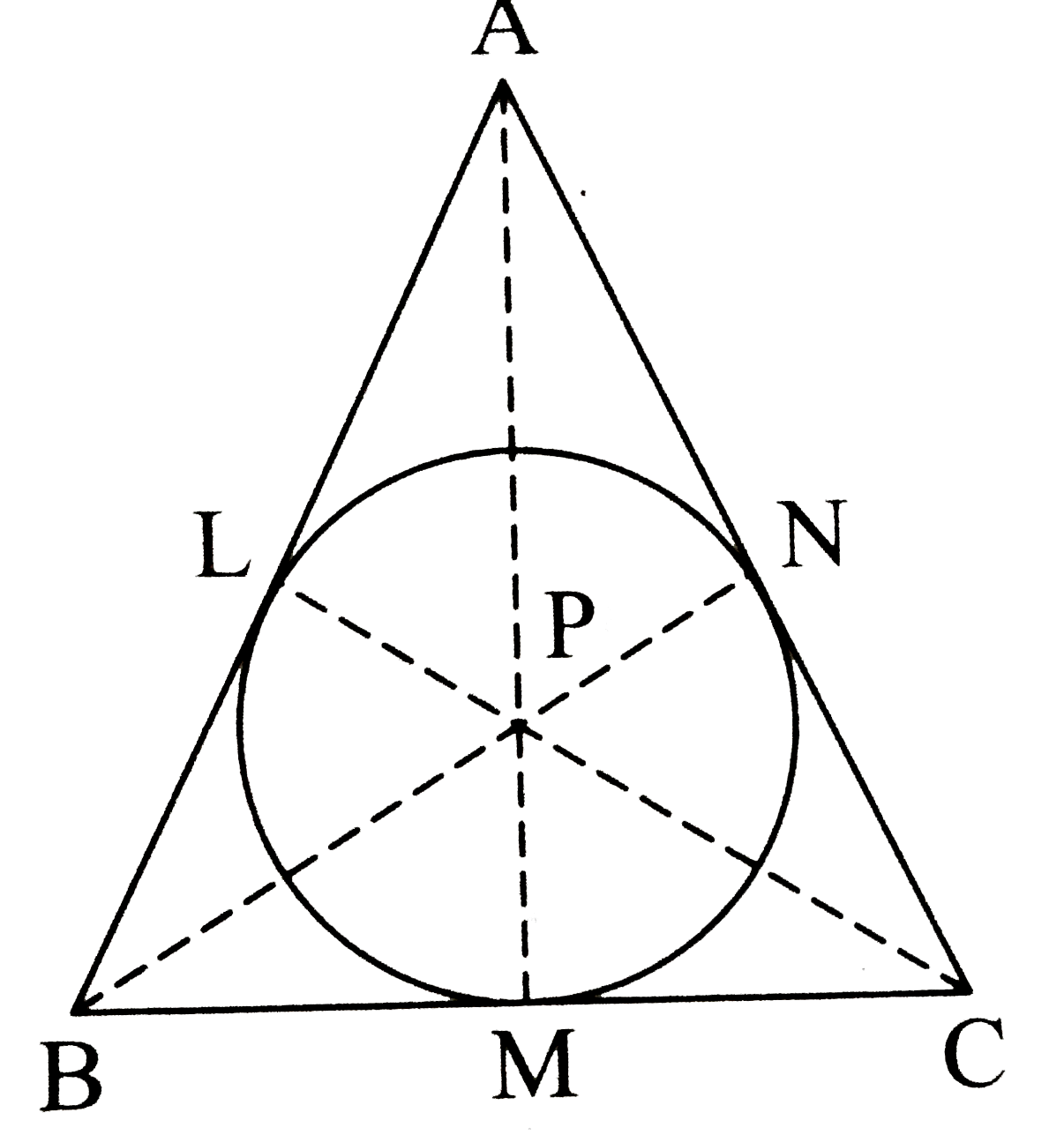
View Solution25. In figure, the sides AB, BC and CA of triangle ABC touch a circle with centre and radius r at P, Q and R respectively. Prove that (i ) AB+CQ=AC+BQ (ii) Area ΔABC=12 perimeter of ΔABC).r.
View SolutionA circle with centre P is inscribed in the ΔABC Side AB, side BC and side A C touch the circle at points L,M and N respectively . Prove that :
A(ΔABC)=12(AB+BC+AC)×r
View Solution