Prove that the tangents at the extremities of any chord make equal angles with the chord.
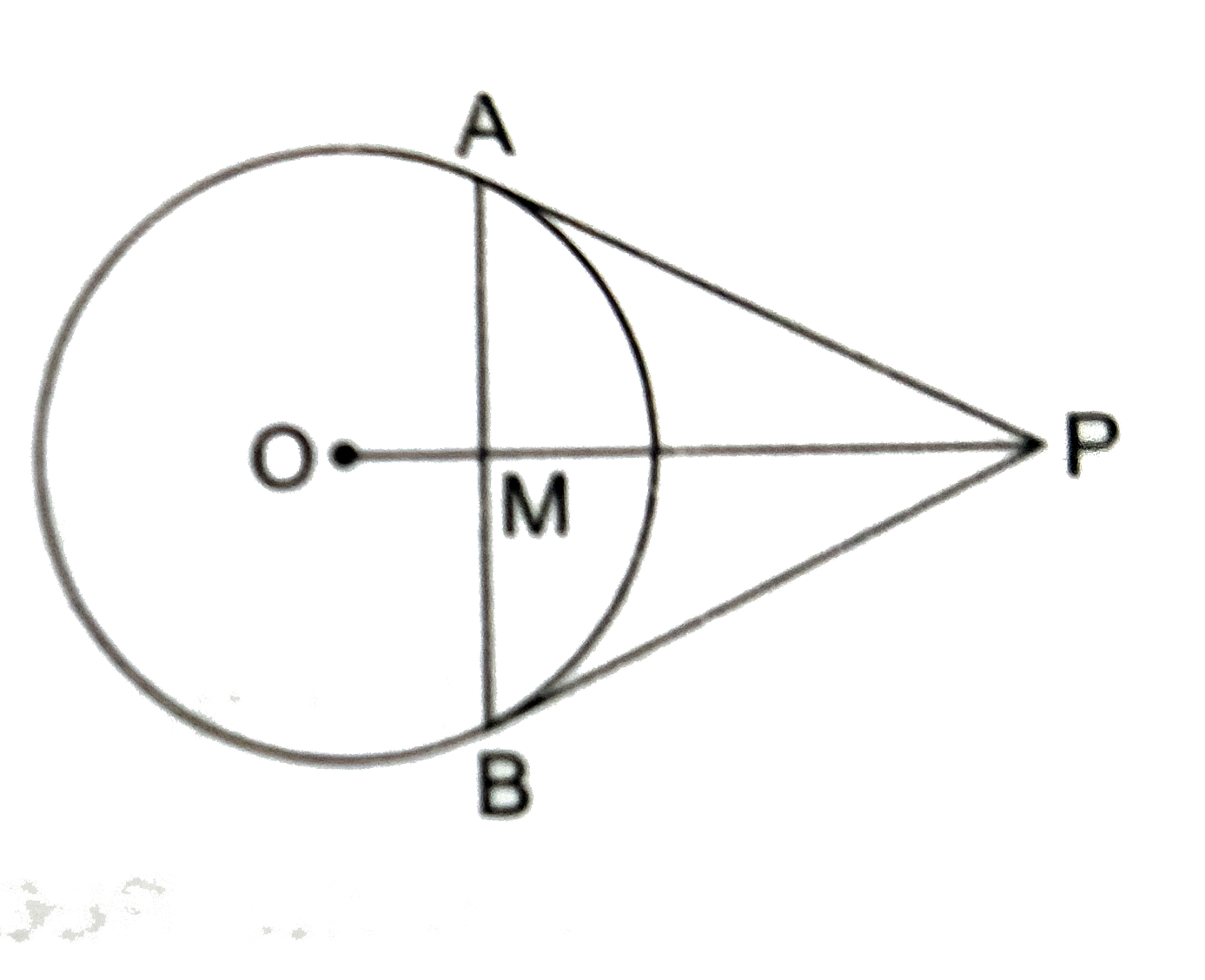
GIVEN AB is any chord of a circle with centre O. Tangents at the extremitites A and B of this chord meet at an external point P. Chord AB intersects the line segment OP at M.
TO PROVE ∠MAP=∠MBP.
PROOF In ΔMAP and ΔMBP, we have
PA=PB [∴ tangents from an external point are equal]
MP=MP [common]
∠MPA=∠MPB [ ∵∠OPA=∠OPB since tangents from an external point are equally inclined to the line segment joining the point to the centre]
∴ΔMAP≅ΔMBP [by SAS-congruence].
And so, ∠MAP=∠MBP [cpct]
Topper's Solved these Questions
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8A
Explore 16 Videos
- CIRCLESBook:RS AGGARWALChapter:CIRCLESExercise:Exercise 8B
Explore 15 Videos
- ARITHMETIC PROGRESSIONBook:RS AGGARWALChapter:ARITHMETIC PROGRESSIONExercise:Multiple Choice Questions (Mcq)
Explore 30 Videos
- CONSTRUCTIONSBook:RS AGGARWALChapter:CONSTRUCTIONSExercise:Test Yourself
Explore 10 Videos
Similar Questions
Knowledge Check
Tangents at the extremities of a focal chord of a parabola intersect on the line
AdirectrixBtangent at vertexCaxis of parabolaDnoneIf the tangent at the extrenities of a chord PQ of a parabola intersect at T, then the distances of the focus of the parabola from the points P.T. Q are in
AAPBGPCHPDNone of these
Prove that the tangent at one extremity of the focal chord of a parabola is parallel to the normal at the other extremity.
View SolutionShow that the locus of the point of intersection of the tangents at the extremities of any focal chord of an ellipse is the directrix corresponding to the focus.
View Solutionprove that the locus of the point of intersection of the tangents at the extremities of any chord of the parabola y2=4ax which subtends a right angle at the vertes is x+4a=0.
View SolutionThe figure shown below consists of the tangents at the extremities of any chord Choose the correct option given below.

View SolutionIf two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View Solution