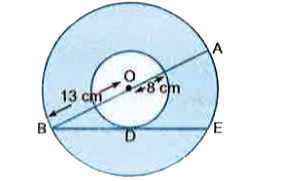
The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.

Video Solution

Text Solution

Verified by Experts

We have $∠ A E B = 90^{\circ}$ [angle in a semicircle]
Also, $O D ⊥ B E$ and $O D$ bisects $B E$ .
In right $Δ O B D$ , we have
$O B^{2} = O D^{2} + B D^{2}$ [by Pythagoras' theorem]
$\Rightarrow B D = \sqrt{O B^{2} - O D^{2}} = \sqrt{13^{2} - 8^{2}} c m$ [ $∵ O B = 13 c m$ , $O D = 8 c m$ ]
$∴ B E = 2 B D = 2 \sqrt{105} c m$ [ $∵ D$ is the midpoint of $B E$ ]
In right $Δ A E B$ , we have
$A B^{2} = A E^{2} + B E^{2}$ [by Pythagoras' theorem]
$\Rightarrow A E = \sqrt{A B^{2} - B E^{2}} = \sqrt{26^{2} - (2 {\sqrt{105}}^{2})} c m = \sqrt{256} c m = 16 c m$
[ $∵ A B =$ diameter $= 2 \times O B = 2 \times 13 c m = 26 c m$ ]
In right $Δ A E D$ , we have
$A D^{2} = A E^{2} + D E^{2}$ [by Pythagoras' theorem]
$\Rightarrow A D = \sqrt{A E^{2} + D E^{2}} = \sqrt{16^{2} + {(\sqrt{105})}^{2}} c m$
$= 19 c m$ $[∵ D E = B D = \sqrt{105} c m]$ .
[Note We can also find $A E$ by using midpoint theorem, since in $Δ A B E$ , $O$ is the midpoint of $A B$ and $D$ is the midpoint of $B E$ and so $O D ∣ ∣ A E$ and $A E = 2 \times O D = 16 c m$ ]

Updated on:21/07/2023

The radii of two concentric circle are 13 cm and 8 cm. AB is a diameter of the bigger circle and BD is a tangent to the smaller circle touching it at D and the bigger circle at E. Point A is joined to D. Find the length of AD.
A20 cm
B19 cm
C18 cm
D17 cm
The radius of two concentric circles are 9 cm and 15 cm. If the chord of the greater circle be a tangent to the smaller circle, then the length of that chord is
A24 cm
B12 cm
C30 cm
D18 cm
If radii of two concentric circles are 4 cm and 5 cm Then the length of the chord of one circle which is tangent to the other circle is
A3 cm
B6 cm
C9 cm
D1 cm