In a class test, the sum of the marks obtained by P in mathematics and science is 28. Had he got 3 more marks in mathematics and 4 marks less in science, the product of marks obtained in the two subjects would have been 180. Find the marks obtained by him in the two subjects separately.
The correct Answer is:Either he got 12 marks in maths and 16 in science or he got 9 marks in maths and 19 in science
To solve the problem step by step, we will define the variables, set up equations based on the information given, and then solve for the marks obtained by P in mathematics and science.
Step 1: Define the Variables
Let:
- x = marks obtained in Mathematics
- y = marks obtained in Science
Step 2: Set Up the Equations
From the problem, we know two things:
1. The sum of the marks in Mathematics and Science is 28:
x+y=28(Equation 1)
2. If P had scored 3 more marks in Mathematics and 4 marks less in Science, the product of the marks would have been 180:
(x+3)(y−4)=180(Equation 2)
Step 3: Substitute y from Equation 1 into Equation 2
From Equation 1, we can express y in terms of x:
y=28−x
Now substitute this into Equation 2:
(x+3)((28−x)−4)=180
This simplifies to:
(x+3)(24−x)=180
Step 4: Expand the Equation
Expanding the left side:
x⋅24−x2+3⋅24−3x=180
This simplifies to:
24x−x2+72−3x=180
Combining like terms gives:
21x−x2+72=180
Step 5: Rearrange the Equation
Rearranging the equation to set it to zero:
−x2+21x+72−180=0
This simplifies to:
−x2+21x−108=0
Multiplying through by -1 to make the leading coefficient positive:
x2−21x+108=0(Equation 3)
Step 6: Factor the Quadratic Equation
Now we need to factor the quadratic equation. We look for two numbers that multiply to 108 and add to -21. The numbers are -12 and -9:
(x−12)(x−9)=0
Step 7: Solve for x
Setting each factor to zero gives us:
1. x−12=0 → x=12
2. x−9=0 → x=9
Step 8: Find Corresponding y Values
Using Equation 1 to find y:
1. If x=12:
y=28−12=16
2. If x=9:
y=28−9=19
Conclusion
The marks obtained by P in Mathematics and Science are:
1. (12,16) or
2. (9,19)
Let:
- x = marks obtained in Mathematics
- y = marks obtained in Science
From the problem, we know two things:
1. The sum of the marks in Mathematics and Science is 28:
x+y=28(Equation 1)
2. If P had scored 3 more marks in Mathematics and 4 marks less in Science, the product of the marks would have been 180:
(x+3)(y−4)=180(Equation 2)
From Equation 1, we can express y in terms of x:
y=28−x
Now substitute this into Equation 2:
(x+3)((28−x)−4)=180
This simplifies to:
(x+3)(24−x)=180
Expanding the left side:
x⋅24−x2+3⋅24−3x=180
This simplifies to:
24x−x2+72−3x=180
Combining like terms gives:
21x−x2+72=180
Rearranging the equation to set it to zero:
−x2+21x+72−180=0
This simplifies to:
−x2+21x−108=0
Multiplying through by -1 to make the leading coefficient positive:
x2−21x+108=0(Equation 3)
Now we need to factor the quadratic equation. We look for two numbers that multiply to 108 and add to -21. The numbers are -12 and -9:
(x−12)(x−9)=0
Setting each factor to zero gives us:
1. x−12=0 → x=12
2. x−9=0 → x=9
Using Equation 1 to find y:
1. If x=12:
y=28−12=16
2. If x=9:
y=28−9=19
The marks obtained by P in Mathematics and Science are:
1. (12,16) or
2. (9,19)
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - Test Yourself55videos
QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - QUADRATIC EQUATIONS EXERCISE - Exercise 4D22videos
QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)37videos
PROBABILITY
- BOOK - RS AGGARWALCHAPTER - REAL NUMBERSEXERCISE - Test Youself20videos
REAL NUMBERS
Similar Questions
In a class test, the sum of the marks obtained by P in mathematics and science is 28. Had he got 3 more marks in mathematics and 4 marks less in science, the product of marks obtained in the two subjects would have been 180. Find the marks obtained by him in the two subjects separately.
View SolutionIn a class test, the sum of the marks obtained by P in Mathematics and science is 28. Had he got 3 marks more in Mathematics and 4 marks less in Science. The product of his marks, would have been 180. Find his marks in the two subjects.
View Solution
Knowledge Check
- Question 1 - Select One
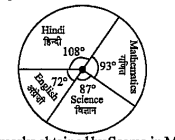
How many marks obtained by Seema in Mathematics?A93B116C109D124 - Question 2 - Select One
What is the difference in the marks obtained by B in English and Mathematics together and the marks obtained by F in the same subjects?
A24B17C15D28 - Question 3 - Select One
The table shows the marks obtained by 25 students in a class test. Find the mean of the marks obtained
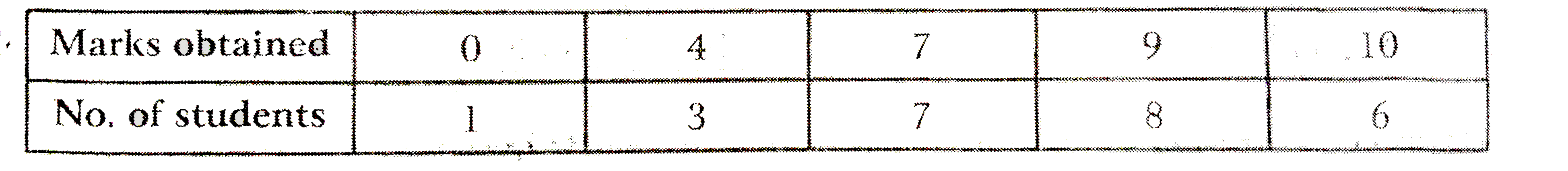 A7.72B7.65C7.4D7
A7.72B7.65C7.4D7
In a class test, the sum of Kamal's marks in mathematics and English is 40. Had he got 3 marks more in mathematics and 4 marks less in English, the product of the marks would have been 360. Find his marks in two subjects separately.
View SolutionIn a class test, the sum of Shelall's marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210 . Find her marks in the two subjects.
View SolutionIn a class test, the sum of Shefalis marks in Mathematics and English is 30. Had she got 2 marks more in Mathematics and 3 marks less in English, the product of their marks would have been 210. Find her marks in the two subjects.
View SolutionIn a class test , the sum of Arun's marks in Hindi and English is 30 . Had he got 2 marks more in Hindi and 3 marks less in English , the product of the marks would have been 210 . Find his marks in the two subjects .
View SolutionWhat is the respective ratio of total marks obtained by Veena and Shreya together in Mathematics to the marks obtained by Rahul in the same subject?
View Solution

