In a school there are two sections, namely A and B, of class X. there are 30 students in section A and 28 students in section B. find the minimum number of books required for their class library so that they can be distributed equally among students of section A ore section B.
To solve the problem of finding the minimum number of books required for the class library so that they can be distributed equally among the students of section A or section B, we need to find the least common multiple (LCM) of the number of students in each section.
1. Identify the number of students in each section:
- Section A has 30 students.
- Section B has 28 students.
2. Find the prime factorization of each number:
- For 30:
- 30 = 2 × 3 × 5
- For 28:
- 28 = 2^2 × 7
3. Determine the LCM using the prime factors:
- The LCM is found by taking the highest power of each prime factor present in the factorizations.
- From the factorizations:
- The highest power of 2 is 2^2 (from 28).
- The highest power of 3 is 3^1 (from 30).
- The highest power of 5 is 5^1 (from 30).
- The highest power of 7 is 7^1 (from 28).
- Therefore, the LCM = 2^2 × 3^1 × 5^1 × 7^1.
4. Calculate the LCM:
- LCM = 4 × 3 × 5 × 7
- First, calculate 4 × 3 = 12.
- Next, calculate 12 × 5 = 60.
- Finally, calculate 60 × 7 = 420.
5. Conclusion:
- The minimum number of books required for their class library so that they can be distributed equally among students of section A or section B is 420.
- Section A has 30 students.
- Section B has 28 students.
- For 30:
- 30 = 2 × 3 × 5
- For 28:
- 28 = 2^2 × 7
- The LCM is found by taking the highest power of each prime factor present in the factorizations.
- From the factorizations:
- The highest power of 2 is 2^2 (from 28).
- The highest power of 3 is 3^1 (from 30).
- The highest power of 5 is 5^1 (from 30).
- The highest power of 7 is 7^1 (from 28).
- Therefore, the LCM = 2^2 × 3^1 × 5^1 × 7^1.
- LCM = 4 × 3 × 5 × 7
- First, calculate 4 × 3 = 12.
- Next, calculate 12 × 5 = 60.
- Finally, calculate 60 × 7 = 420.
- The minimum number of books required for their class library so that they can be distributed equally among students of section A or section B is 420.
Topper's Solved these Questions
- REAL NUMBERSBook:RS AGGARWALChapter:REAL NUMBERSExercise:Exercise 1A
Explore 10 Videos
- REAL NUMBERSBook:RS AGGARWALChapter:REAL NUMBERSExercise:Exercise 1B
Explore 27 Videos
- QUADRATIC EQUATIONS Book:RS AGGARWALChapter:QUADRATIC EQUATIONS Exercise:Test Yourself
Explore 55 Videos
- SAMPLE PAPER IBook:RS AGGARWALChapter:SAMPLE PAPER IExercise:SECTION D
Explore 16 Videos
Similar Questions
In a school there are two sections section A and section B of class X . There are 32 students in section A and 36 students in section B . Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B .
View SolutionIn a school there are two sections- section A and section B of classX, There are 32 students in section A. 36 students in section B. Determine the minimum number of books required for their class library so that they can be distributed equally among students of section A or section B
View Solution
Knowledge Check
The average score of two serctions is 28. The average score of section A is 30, which there are 25 students, If there are 20 students in section B,then the average score of section B is
A25.5B27.5C29D33A class is divided into two sections A and B . Passing average of 20 students of section A is 80% and passing average of 30 students of section B is 70% . What is the passing average of both the sections ?
A0.72B0.74C0.75D0.77Read the data given below and answer the questions based on it.
There were 3 sections namely A, B and C in a test. Out of three 33 students passed in section A, 34 students passed in Section B and 32 passed in Section C. 10 students passed in Section A and Section B, 9 passed in Section B and Section C, 8 passed in Section A and Section C. The number of students who passed each section alone was equal and was 21 for each section.
The ratio of the number of students passed in one or more of the sections to the number of students who passed in section A alone is :
A. 78/21
B. 3
C. 73/21
D. 75/21ABBDCCDA
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section Bof grade X. There are 32 students in section A and 36 students in section B.

What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?
View SolutionTo enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section Bof grade X. There are 32 students in section A and 36 students in section B.

If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32 , 36) is
View SolutionIn a school, there are five sections of Class VI. The number of students in each section is given below:
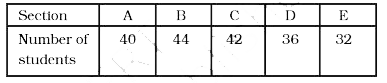
Represent the above data using a bar graph.
View SolutionTo enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section Bof grade X. There are 32 students in section A and 36 students in section B.

If p and q are positive integers such that p=ab2andq=a2b , where a , b are prime numbers, then the LCM (p, q) is
View SolutionIf the average marks of 30 students of section A is 55 and the average marks of 30 students of section B is 60 ,then find the combined average of both the sections.
View Solution

