A rhombus-shaped sheet with perimerter 40 cm and on e diagonal 12 cm, is painted on both sides at the rate of Rs. 5 per cm2. Find the cost of painting.
The correct Answer is:Rs. 960
To find the cost of painting a rhombus-shaped sheet with a perimeter of 40 cm and one diagonal of 12 cm, we can follow these steps:
Step 1: Find the length of one side of the rhombus.
The perimeter of a rhombus is given by the formula:
Perimeter=4×side
Given that the perimeter is 40 cm, we can set up the equation:
4×side=40
Dividing both sides by 4 gives:
side=10 cm
Step 2: Find the length of the other diagonal.
In a rhombus, the diagonals bisect each other at right angles. Let the length of the other diagonal be d2. We know one diagonal d1=12 cm. The diagonals divide the rhombus into four right-angled triangles.
Using the Pythagorean theorem in one of the triangles formed by the diagonals, we have:
(d12)2+(d22)2=side2
Substituting the known values:
(122)2+(d22)2=102
This simplifies to:
62+(d22)2=100
36+(d22)2=100
Subtracting 36 from both sides:
(d22)2=64
Taking the square root:
d22=8⇒d2=16 cm
Step 3: Calculate the area of the rhombus.
The area A of a rhombus can be calculated using the formula:
A=12×d1×d2
Substituting the values of the diagonals:
A=12×12×16
Calculating this gives:
A=12×192=96 cm2
Step 4: Calculate the cost of painting.
Since the sheet is painted on both sides, the total area to be painted is:
Total Area=2×A=2×96=192 cm2
The cost of painting is given at the rate of Rs. 5 per cm². Therefore, the total cost C is:
C=192×5=960 Rs.
Final Answer:
The cost of painting the rhombus-shaped sheet is Rs. 960.
---
The perimeter of a rhombus is given by the formula:
Perimeter=4×side
Given that the perimeter is 40 cm, we can set up the equation:
4×side=40
Dividing both sides by 4 gives:
side=10 cm
In a rhombus, the diagonals bisect each other at right angles. Let the length of the other diagonal be d2. We know one diagonal d1=12 cm. The diagonals divide the rhombus into four right-angled triangles.
(d12)2+(d22)2=side2
Substituting the known values:
(122)2+(d22)2=102
This simplifies to:
62+(d22)2=100
36+(d22)2=100
Subtracting 36 from both sides:
(d22)2=64
Taking the square root:
d22=8⇒d2=16 cm
The area A of a rhombus can be calculated using the formula:
A=12×d1×d2
Substituting the values of the diagonals:
A=12×12×16
Calculating this gives:
A=12×192=96 cm2
Since the sheet is painted on both sides, the total area to be painted is:
Total Area=2×A=2×96=192 cm2
The cost of painting is given at the rate of Rs. 5 per cm². Therefore, the total cost C is:
C=192×5=960 Rs.
The cost of painting the rhombus-shaped sheet is Rs. 960.
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - EXERCISE12videos
AREAS OF TRIANGLES AND QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - EXAMPLE6videos
AREAS OF TRIANGLES AND QUADRILATERALS
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE5videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B16videos
BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGON
Similar Questions
A rhombus shaped sheet with perimeter 40cm and one diagonal 12cm, is painted on both sides at the rate of rupee 5 per cm2. Find the cost of painting.
View SolutionA rhombus sheet, whose perimeter is 32m and whose one diagonal is 10m long, is painted on both sides at the rate of Rs. 5 per m2 . Find the cost of painting.
View Solution
Knowledge Check
- Question 1 - Select One
The side of a rhombus are 10 cm and one of its diagonals is 16 cm . The area of the rhombus is :
A72B48C96D192 - Question 2 - Select One
A sheet in the form of a rhombus whose diagonals are 10 m and 8 m. The cost of painting both of its surfaces at the rate of Rs 70 per m2 is
ARs 5600BRs 4000CRs 2800DRs 2000 - Question 3 - Select One
The side of a rhombus is 10 cm and one diagonal is 16 cm. The area of the rhombus is
A96 cm2B95 cm2C94 cm2D93 cm2
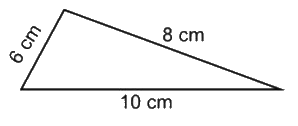
The cost of painting the given sign board at the rate of 9 paise per cm2 isView SolutionFind the cost of painting at the rate of Rs.5.60perm2 on the hemispherical dome of diameter 10 m.
View SolutionThe sides of a triangle shaped sheet are 5cm, 12cm and 13cm. Find the cost of painting on the sheet at the rate of Rs 30 per cm2?
View SolutionA thin metal iron sheet is rhombus in shape with each side of 10 m. If one of its diagonals is 16m. find the cost of painting its both sides at Rs.6perm2 Also, find the distance between the sides of the rhombus
View SolutionThe side of a triangle shaped sheet are 5cm, 12cm and 13cm. Find the cost of painting on the sheet at the rate of Rs 30 per cm sq.
View Solution

