Find the area of the quadrilateral ABCD in which AB = 9 m, BC = 40 m, ∠ABC=90∘, CD = 15 m and AD = 28 m.
Video Solution
Text Solution
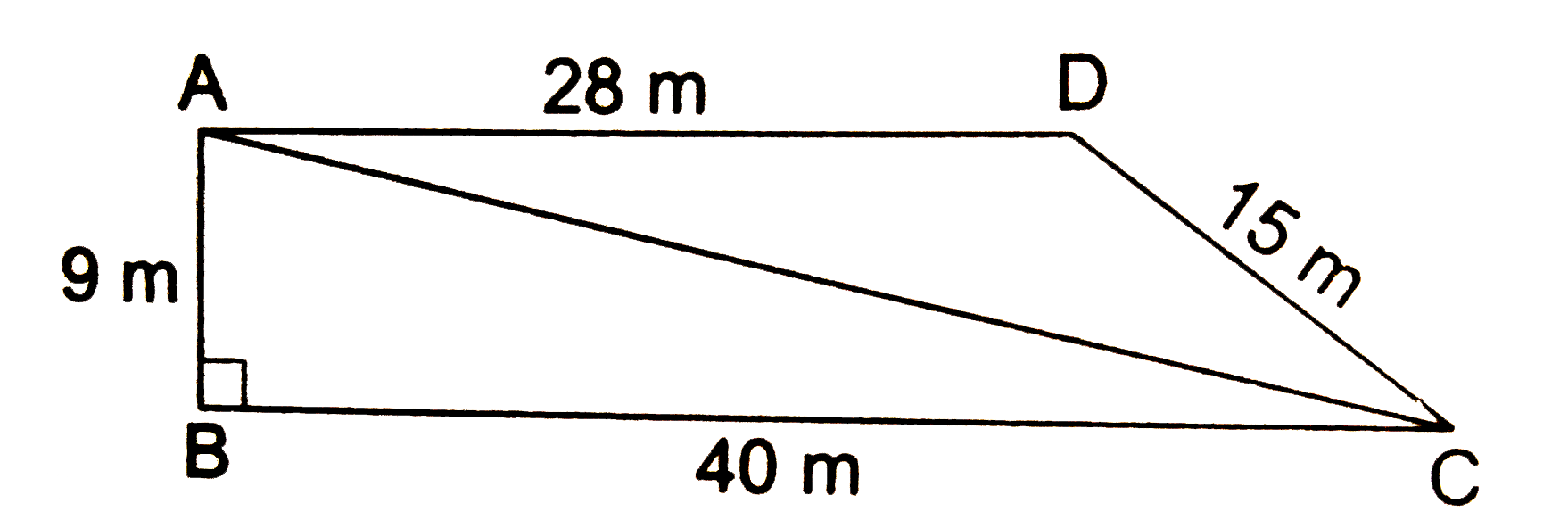
Area of right ΔABC
=(12×base×height)
=(12×40×9)m2=180m2.
Also, from right ΔABC, we get
AC2=AB2+BC2
=[(9)2+(40)2]m2
=(81+1600)m2=1681m2
⇒ AC=√1681m=41m
In ΔACD, we have AC = 41 m, CD = 15 m and AD = 28 m.
Let a = 41 m, b = 15 m and c = 28 m. Then,
s=12(41+15+28)m=(12×84)m=42m.
∴ (s−a)=(42−41)m=1m,(s−b)=(42−15)m=27mand(s−c)=(42−28)m=14m.
∴ area of ΔACD=√s(s−a)(s−b)(s−c)
=√42×1×27×14m2
=(14×9)m2=126m2.
Area of the quad. ABCD = area(ΔABC) + area(ΔACD)
=(180+126)m2=306m2.
|
Topper's Solved these Questions
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - EXAMPLE
6 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Exercise 14
32 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
Similar Questions
Knowledge Check
A park is in the shape of quadrilateral ABCD in which AB=9cm,BC=12cm,CD=5cm,AD=8cm and ∠C=90∘. Find the area of the park.
A65.4cm2B69.4cm2C66.4cm2D68.4cm2
Find the area of the quadrilateral ABCD , in which AB=7cm,BC=6cm,CD=12cm,DA=15cmandAC=9cm
View SolutionFind the area of quadrilateral ABCD in which ∠B=90∘, BC = 32 cm, AB = 24 cm and CD=DA = 25 cm.
View SolutionFind the area of the quadrilateral ABCD; in which AB = 7 cm; BC =6 cm;CD =12 cm; DA= 15 cm and AC =9 cm
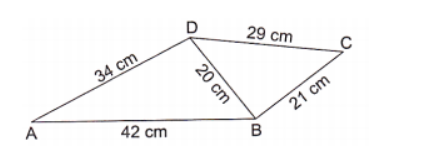
View SolutionFind the area of the quadrilateral ABCD in which in AB = 42 cm, BC = 21 cm, CD = 29 cm, DA = 34 cm and diagonal BD = 20 cm.
View SolutionConstruct a quadrilateral ABCD in which AB=5cm, Ac=6cm, AD=8cm and ∠ABC=∠ACD=90∘.
View SolutionConstruct a quadrilateral ABCD in which AB=2.9cm,BC=3.7cm, CD=4.2cm, AD=6.1 and ∠B=90∘.
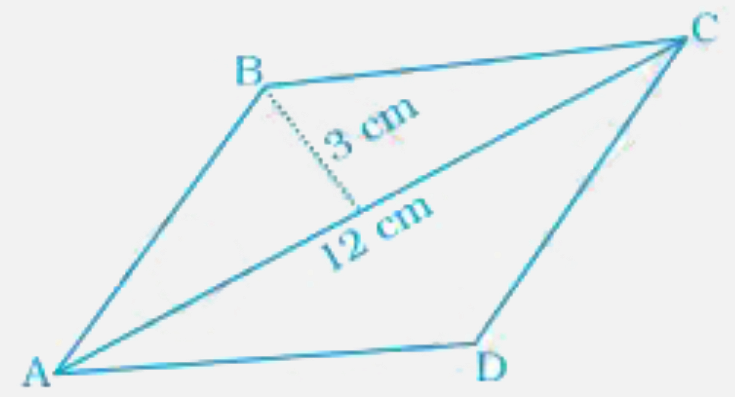
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View Solution
