In the given figure, ABCD is a rhombus. Then,
A
AC2+BD2=AB2
B
AC2+BD2=2AB2
C
AC2+BD2=4AB2
D
2(AC2+BD2)=3AB2
Video Solution
Text Solution
The correct Answer is:C
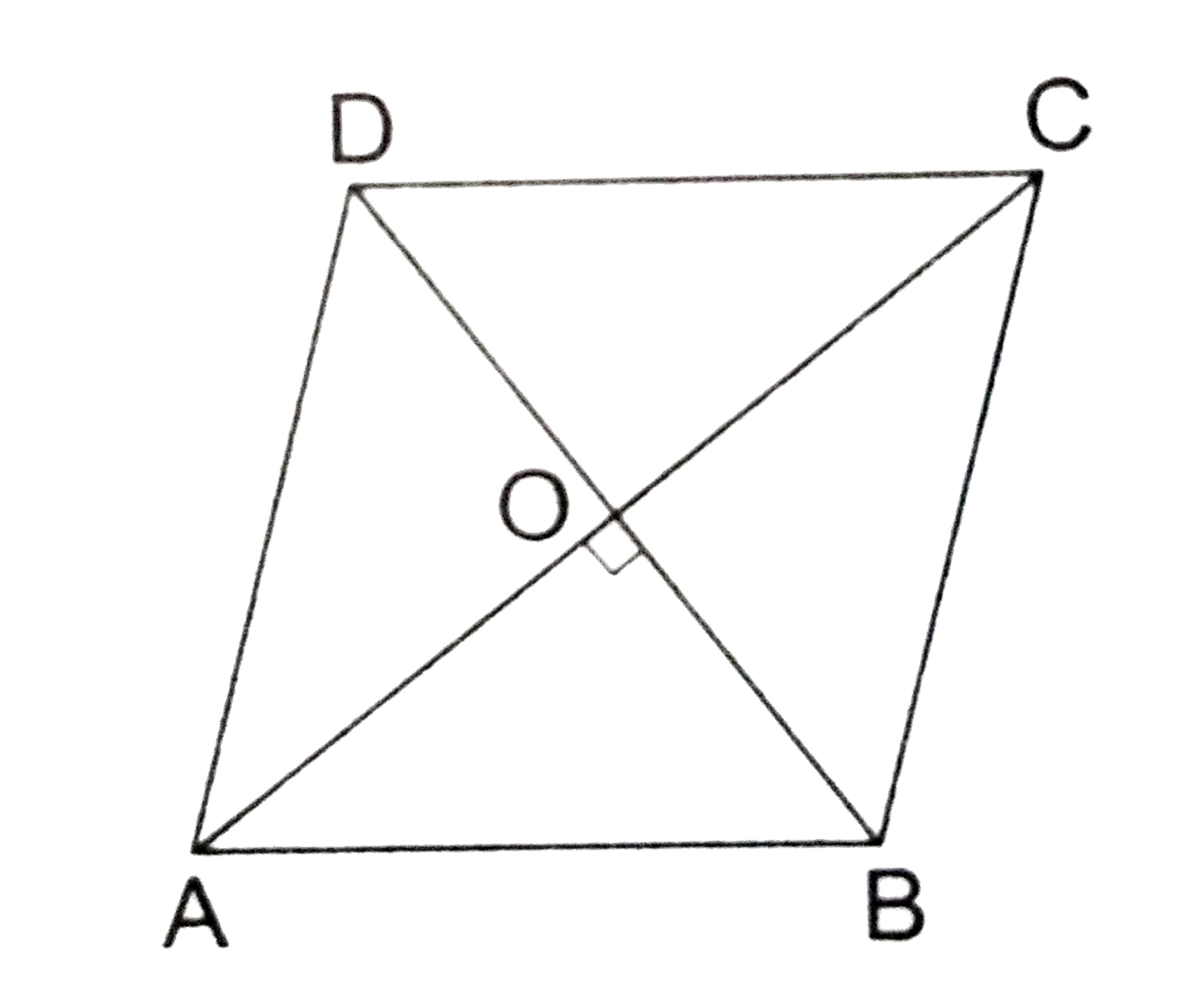
We known that the diagonals of a rhombus bisect each other at right angles.
∴OA=12AC,OB=12BDand∠AOB=90∘
∴AB2=OA2+OB2=14AC2+14BD2
r∀rr4AB2=(AC2+BD2).
|
Topper's Solved these Questions
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Short-Answer Questions
1 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Assertion - and - Reason Type MCQ
4 Videos
- QUADRILATERALSBOOK - RS AGGARWALCHAPTER - QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
47 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
10 Videos
Similar Questions
Knowledge Check
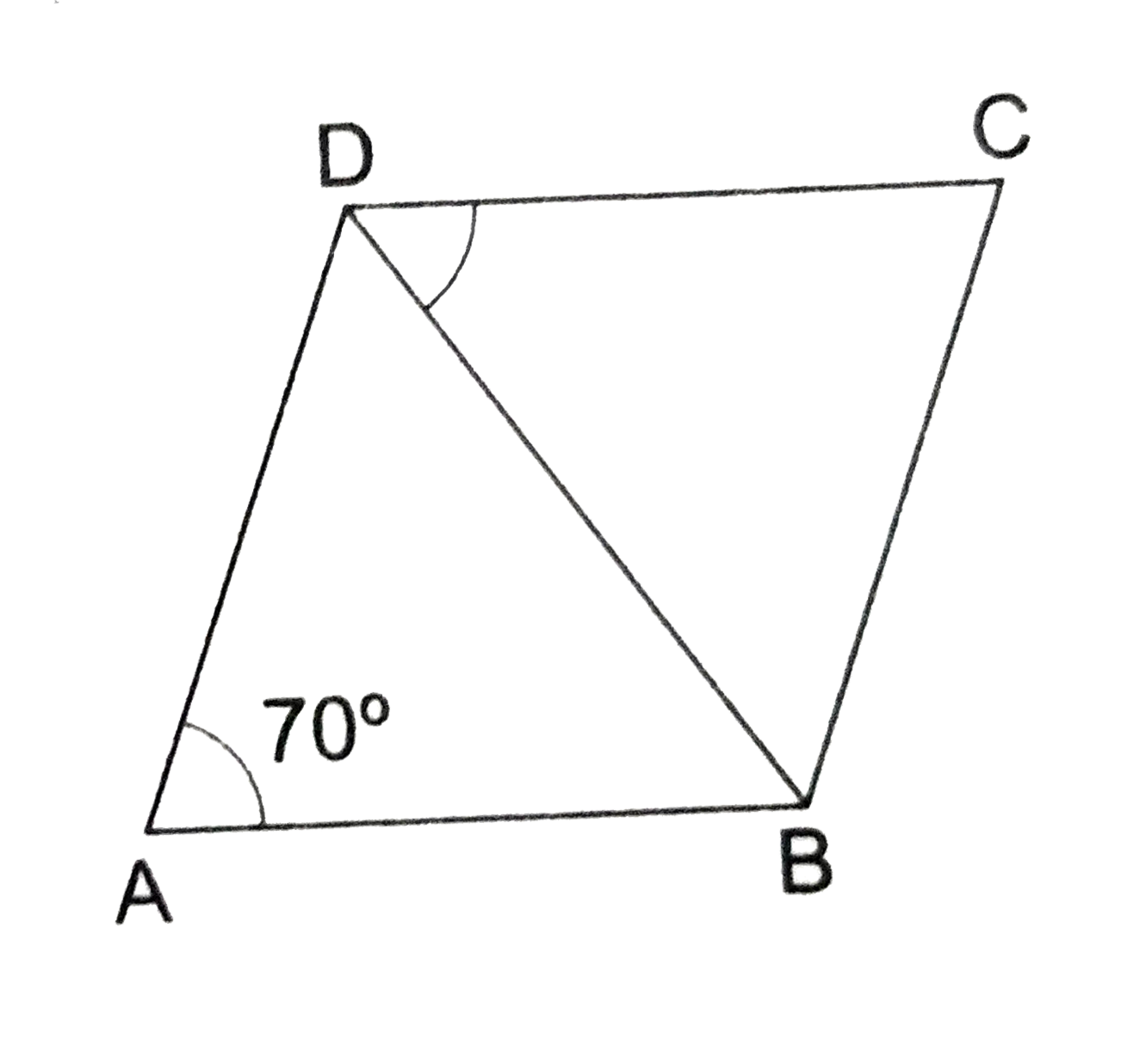
In the given figure, ABCD is a rhombus. If ∠A=70∘, then ∠CDB is equal to
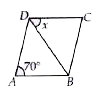 A65∘B55∘C75∘D80∘
A65∘B55∘C75∘D80∘If ABCD is a rhombus, then
AAC2+BD2=6AB2BAC2+BD2=5AB2CAC2+BD2=4AB2DAC2+BD2=3AB2If ABCD is a rhombus, then
AAC2+BD2=AB2BAC2+BD2=2AB2CAC2+BD2=4AB2DAC2+BD2=3AB2
If ABCD is a rhombus, then :
View SolutionIf ABCD is a rhombus, then :
View SolutionIn the given figure PQRS is a rhombus, then the value of x is
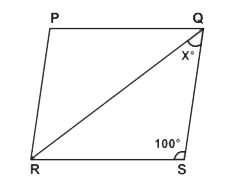
View SolutionIn the adjoining figure, ABCD is a rhombus and ABE is an equilateral triangle. If ∠BCD=70∘, find
(a)∠ADE (b)∠BDE (c)∠BED

View SolutionIn the given diagram, ABCD is a rhombus, AEC and BED are straight lines.
p+q+r+s+t=?
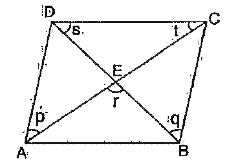
View Solution