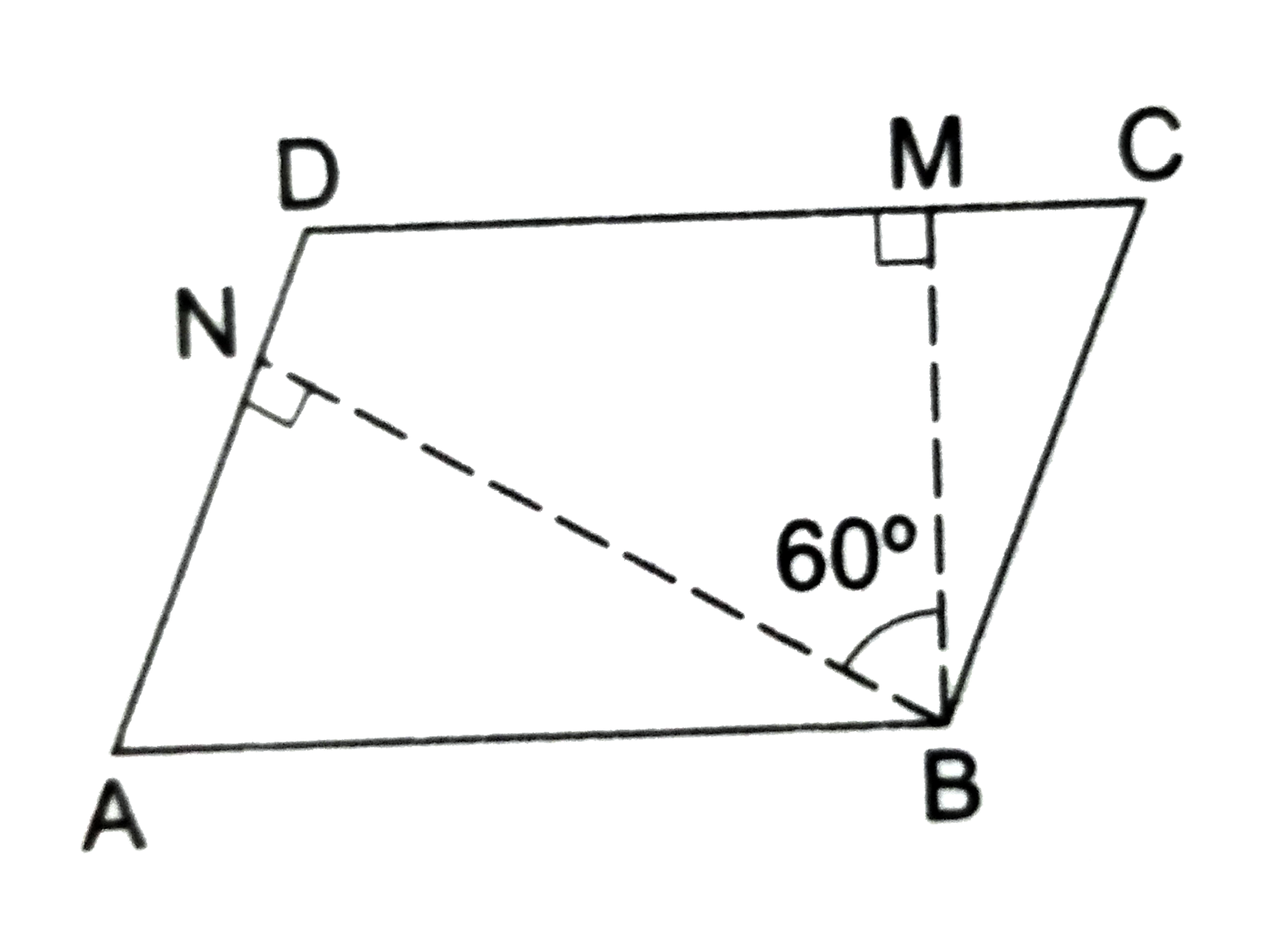
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 600. Find the angles of parallelogram.
The correct Answer is:60∘,120∘,60∘,120∘
∠ABM=90∘and∠MBN=60∘⇒∠ABN=30∘.
In △ABN, we have ∠A=60∘.
And so, ∠B=120∘,∠C=60∘,∠D=120∘.
Similar Questions
The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 600. Find the angles of parallelogram.
View SolutionThe angle between two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 60∘. Find the angles of the parallelogram.
View Solution
Knowledge Check
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle is 50∘ . The two adjacent angles of parallelogram are
A50∘,130∘B60∘,120∘C55∘,125∘D70∘,110∘Consecutive angles of parallelogram are
AEqualBComplimentaryCSupplementaryDNone of these
The angle between the two altitudes of a parallelogram through the vertex of an obtuse angle of the parallelogram is 45°. Find the angles of the parallelogram.
View SolutionThe angle between the two altitudes of a parallelogram through the same vertex of an obtuse angle of the parallelogram is 30°. The measure of the obtuse angle is
View SolutionThe sum of two opposite angles of a parallelogram is 130∘. Find all the angles of the parallelogram.
View SolutionThe sum of adjacent angles of a parallelogram is
View SolutionOne angle of a parallelogram is 60∘. Find its remaining angles.
View SolutionTwo adjacent angles of a parallelogram are as 1:2. Find the measures of all the angles of the parallelogram.
View Solution
