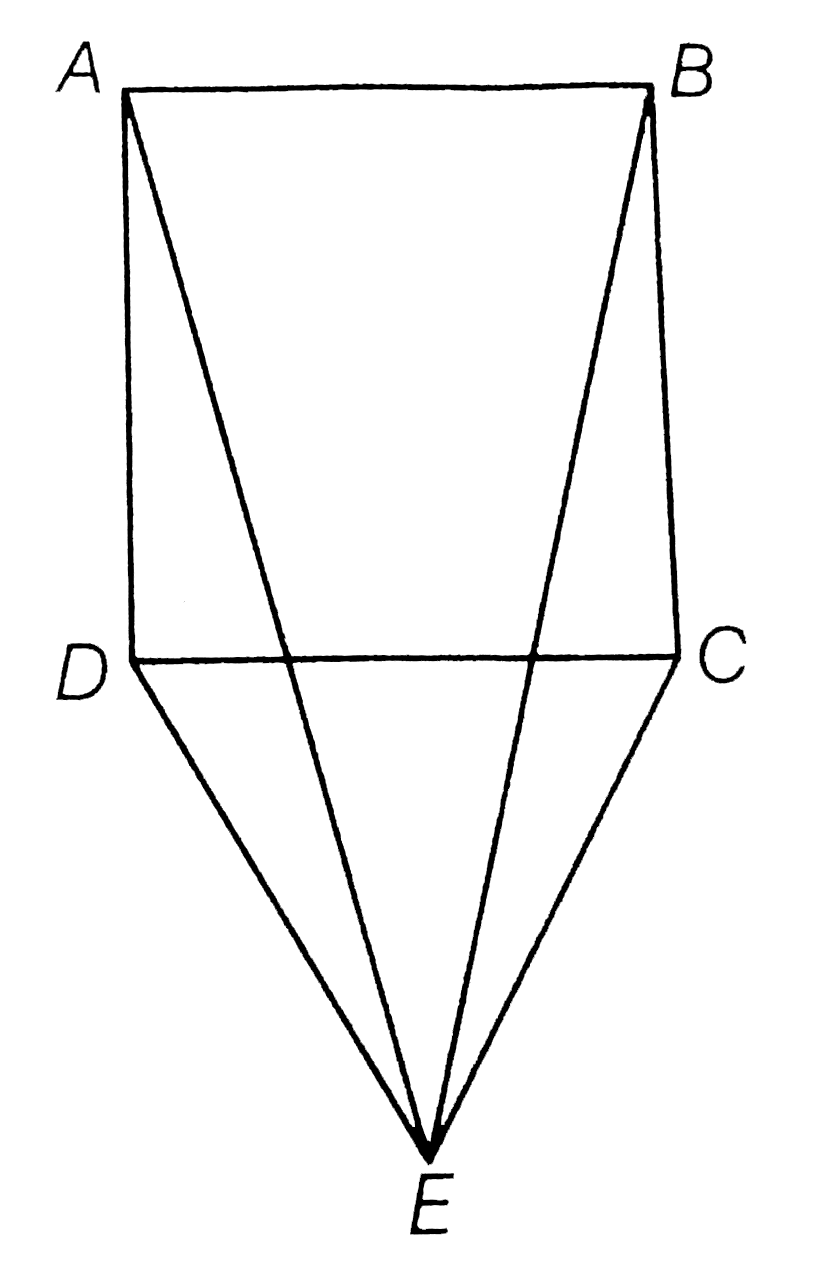
In the adjoining figure, ABCD is a square and △EDC is an equilateral triangle. Proove that
(i) AE=BE, (ii) ∠DAE=15∘.

Video Solution
Text Solution
△ADE≅△BCE [∵AD=BC,DE=CE,∠ADE=∠BCE=(90∘+60∘)]
∴AE=BE.
Now, ∠ADE=150∘andDA=DE⇒∠DAE=∠DEA=15∘.
|
Similar Questions
Knowledge Check
ABCD is a square and ABE is an equilateral triangle outside the square then
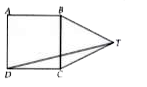
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseIn the given diagram, ABCD is a square and Δ BCT is an equilateral triangle. ∠ BTD equals
 A30∘B15∘C45∘D35∘
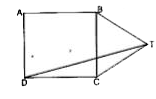
A30∘B15∘C45∘D35∘In the given figure,ΔCDE is an equlatel triangle triangle formed on a side CD of a square ABCD.Show that ΔADE≅ΔBCE.
 ARHSBSSSCAASDSAS
ARHSBSSSCAASDSAS
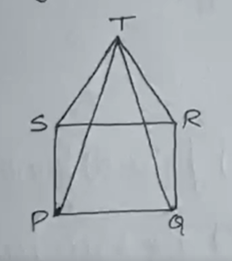
Find the perimeter of the given figure : BCDE is a square and ABC is an equilateral triangle.

View SolutionIn the figure below, ABCD is a square , MDC is an equilateral triangle. Find the value of x.
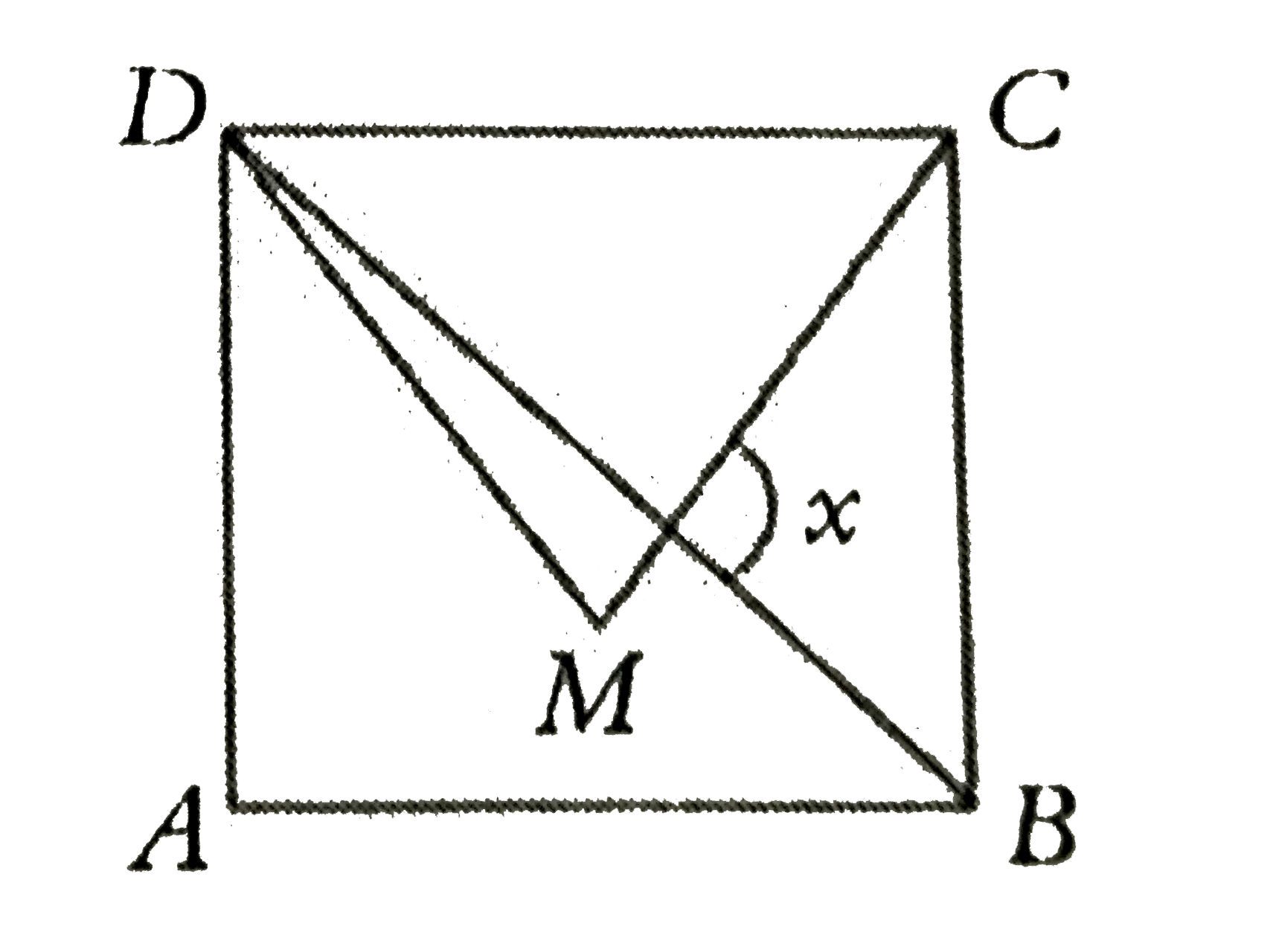
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP

View SolutionABCD is a square and AOB is an equilateral triangle. What is the value of ∠DOC?
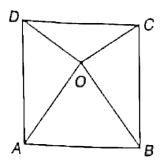
View SolutionAngle of rotation of an equilateral triangle is
View Solution