The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

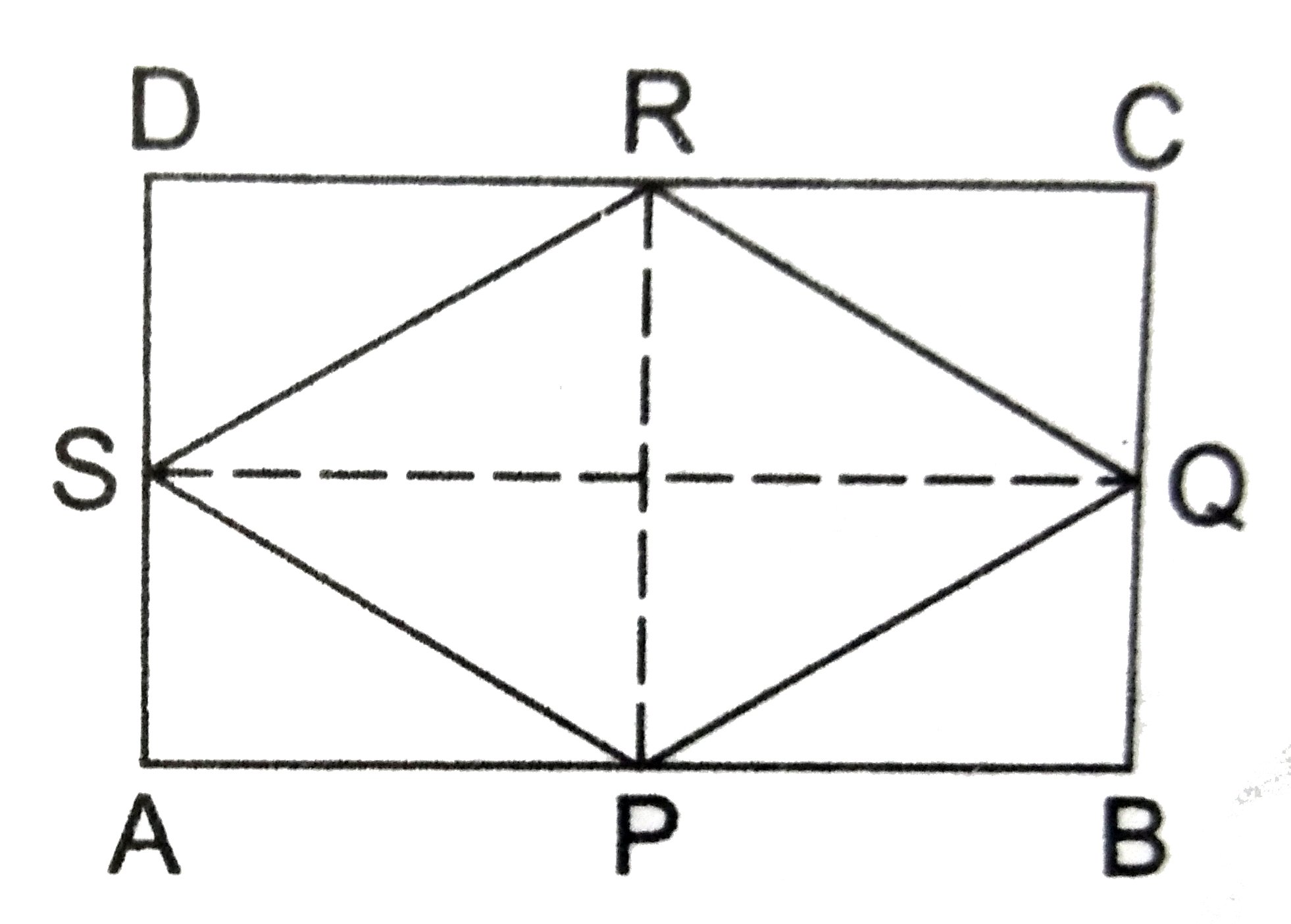
ocr_image
Let ABCD be a quadrilateral in which P, Q, R, S are the midpoints of AB, BC, CD and DA respectively. Join AC.
In △ABC, the points P and Q are the midpoints of AB and BC respectively.
∴ PQ ||AC and PQ=12AC (by midpoint theorem).
Again , in △ DAC, the points S and R are the midpoints of AD and DC respectively.
∴ SR||AC and SR=12AC (by midpoint theorem).
Now, PQ||AC and and SR||AC ⇒ PQ||SR.
Also, PQ=SR (each equal to 12AC).
∴ PQ||SR and PQ=SR.
Hence, PQRS is a parallelogram.

Updated on:21/07/2023
|
Class 9MATHSQUADRILATERALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The figure formed by joining the mid-points of adjacent sides of a rhombus is

    Aa square
    Brectangle
    Ctrapezium
    Dnone of these

  • The figure formed by joining the mid-points of the sides of a quadrilateral taken in order is

    Aparallelogram
    Brectange
    Csquare
    Dnone

  • Consider the following statements
    1. The bisectors of all the four angles of a parallelogram enclose a rectangle.
    2. The figure formed by joining the midpoints of the adjacent sides of a rectangle is a rhombus.
    3. The figure formed by joining the midpoints of the adjacent sides of a rhombus is a square.
    Which of these statements are correct ?

    A1 and 2
    B2 and 3
    C3 and 1
    D1, 2 and 3