In the adjoining figure, BC is a diameter of a circle with centre O. If AB and CD are two chords such that AB ∣∣ CD, prove that AB=CD
Video Solution
Text Solution
Draw OL⊥AB and OM⊥CD
∴ΔOLB≅ΔOMC[∵∠OBL=∠OCL,OB=OC=r and ∠OLB=∠OMC=90∘ ]
∴OL=OM.
But, the chords equidistant from the centre are equal.
Hence, AB = CD.
|
Similar Questions
Knowledge Check
In a circle with centre P.AB and CD are congruent chords. If ∠PAB=40∘, then ∠CPD=
A40∘B80∘C100∘D50∘In the adjoining figure AB∣∣CDandPQ=SR, then :
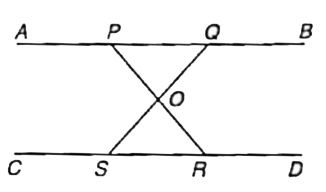 APQ=PSBSR=RPCPS=QRDAP=RD
APQ=PSBSR=RPCPS=QRDAP=RDAB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
A42∘B30∘C60∘D35∘
In the adjoining figure, O is the centre of a circle in which AB and CD are two diameters. Prove that AC| |BD and AD| |BC. If ∠OBD=50∘, then find the value of ∠AOC.

View SolutionAB and CD are diameters of a circle with centre O. If ∠OBD=50∘ then find ∠AOC
View SolutionIn the adjoining figure, O is the centre of the circle. AB and CD are equal chords.
If ∠AOB=100∘, then find ∠CED.
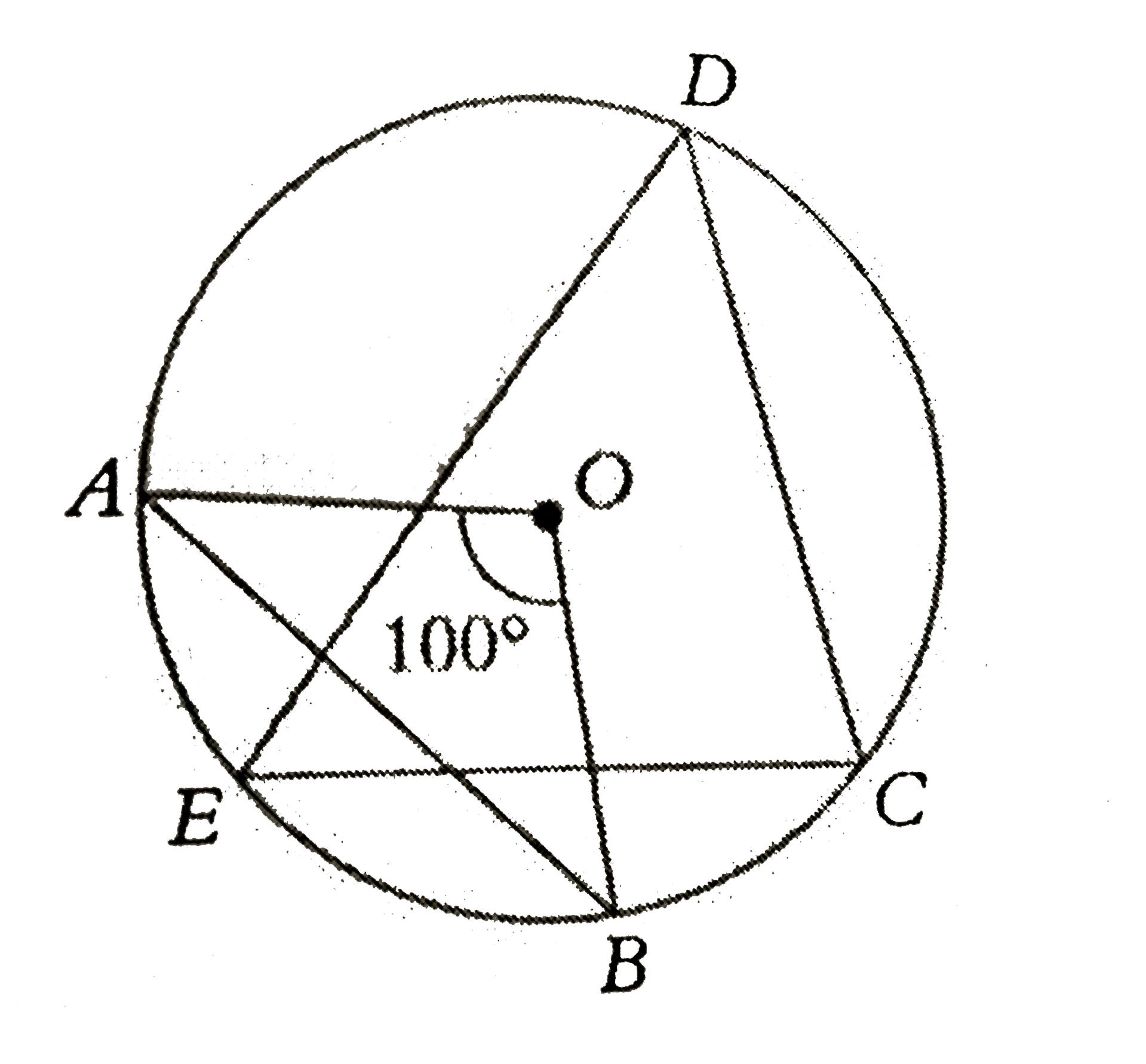
View SolutionIn the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
View SolutionIn a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
View Solution

